Esta segunda parte de la serie Casualidad y Causalidad (aquí está la primera parte) casi no sale. He tenido mucha movida magufa últimamente -y lo que me queda-, y además, cuando voy a buscar el borrador de este artículo en blogger.com, ¡ha desaparecido! Al parecer, estoy gafado. O a lo mejor se trata de la ley de Murphy: si algo puede salir mal, entonces saldrá mal. Sigamos, por tanto, y vamos a intentar romper tan implacable relación de causalidad.
Uno de los problemas a la hora de intentar establecer una relación causal es el «filtrado selectivo»: no tenemos en cuenta ciertos datos, bien porque no concuerden con nuestra teoría, bien porque, sencillamente, los creamos irrelevantes. Una irrelevancia de este tipo le costó a la NASA un transbordador y siete astronautas.
El 28 de enero de 1986, el transbordador Challenger despegó de Cabo Cañaveral. Dos minutos después, sus piezas dispersas caían al mar entre estelas de humo. Para averiguar las causas del accidente, se reunió una comisión que incluía nombres como Neil Armstrong, Charles «Chuck» Yeager … y el profesor Richard Feynman, un favorito de este blog. En una famosa aparición televisiva, Feynman apuntó a los problemas de elasticidad de un elemento llamado Anillo O, que unía las juntas de los motores de combustible sólido. Según se determinó después, la baja elasticidad del anillo O hizo que dejase escapar gases calientes, causando una enorme explosión. Feynman mostró cómo, tras meter un anillo de goma en agua helada, tardaba unos críticos segundos en recuperar la forma original. Recientemente, Amazings nos recordó la intervención de Feynman en el asunto (he aquí el artículo).
De inmediato surge la pregunta: ¿es que la NASA no estaba al tanto de este problema? Por supuesto que sí, e hicieron multitud de pruebas antes de que volase el primer pájaro. La conclusión de los fabricantes fue que había margen de seguridad. Aunque no todos compartían esta afirmación. Un memorándum interno del fabricante Morton Thiokol, escrito seis meses antes del accidente, afirma que «si no tomamos medidas inmediatas para dedicar un equipo a resolver el problema [de erosión en los anillos O] … corremos el riesgo de perder un vuelo junto con todas las instalaciones de lanzamiento»
Richard Feynman fue más contundente con sus palabras: «[El proceso de toma de decisiones fue] una especie de ruleta rusa … [El transbordador] vuela [con erosión en los anillos O] y no pasa nada. Entonces se sugiere que el riesgo no es tan alto para el siguiente vuelo. Podemos relajar un poco los estándares porque nos hemos salido con la nuestra esta vez …»
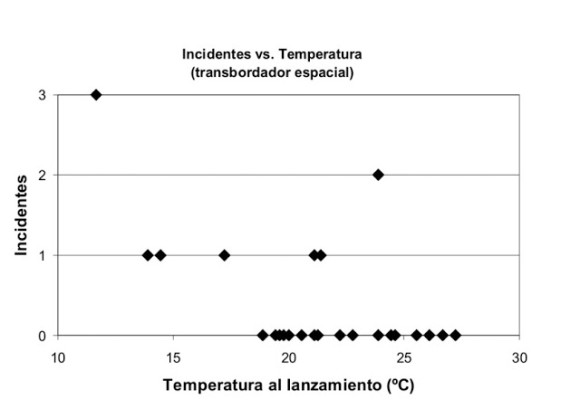
«Salirse con la suya» era algo que aparentemente se derivaba de la siguiente gráfica, en la que se muestra el número de incidentes ocurridos en vuelos de transbordador, como función de la temperatura de los anillos O en el momento del despegue: [Fuente: Report of the Presidential Commission on the Space Shuttle Challenger Accident, Volumen 1, página 146, Figura 6. Adaptación de Arturo Quirantes]
[Fuente: Report of the Presidential Commission on the Space Shuttle Challenger Accident, Volumen 1, página 146, Figura 6. Adaptación de Arturo Quirantes]
En esta gráfica hay muy pocos puntos. El que está más a la izquierda muestra tres incidentes a una temperatura de unos 12ºC. Se trató del vuelo STS-51C que efectuó otro transbordador (el Discovery). Hay otro con dos incidentes, a 24ºC (vuelo STS-61A, Challenger). No parece haber una relación entre número de fallos y temperatura, y por eso se pensó que todo iría bien.
Pero los expertos cometieron un error fatal. Preocupados por la temperatura cuando había incidentes, se olvidaron de los vuelos en los que no hubo incidentes. Si los añadimos a la gráfica, obtenemos esto:
[Fuente: Report of the Presidential Commission on the Space Shuttle Challenger Accident, Volumen 1, página 146, Figura 7. Adaptación de Arturo Quirantes]
Ahora el panorama cambia radicalmente. La nueva información de que disponemos nos indica que, por debajo de 19ºC, podemos tener problemas. Eso no nos asegura un vuelo feliz (hubo dos incidentes a 24ºC, recuerden). Pero la línea de puntos de cero incidentes nos da una receta bien clara: si bajas de los 19 grados, tendrás problemas. El propio informe de la Comisión del Challenger fue claro: «la consideración de toda la historia de temperatura de lanzamientos indica de que la probabilidad de fallo del anillo O aumenta hasta casi una certidumbre total si la temperatura de la junta es menor de 65ºF [18.3ºC]»
La temperatura de los anillos O del Challenger en el momento de su último despegue fue de dos grados centígrados bajo cero.
Una vez hemos establecido que dos sucesos A y B están relacionados entre sí, podemos arriesgarnos y afirmar que A => B, es decir, que A es el agente causante y B es la consecuencia. En el ejemplo del Challenger, creo que está claro: la causa es la baja temperatura, y la consecuencia es la aparición de fallos. No es al revés. Sin embargo, en muchos otros casos no es tan evidente. Una de las cosas que más me hace chirriar los dientes es ver en un medio de comunicación una relación de causalidad cuyo orden es caprichoso. O dicho en otras palabras, ¿qué causa qué? Lo que nos lleva a la primera alternativa.
Alternativa 1: B es la causa y A es la consecuencia.
Pongamos un ejemplo. Digamos que el Partido Famoso (PF) ha obtenido mayoría absoluta en las comunidades más ricas de este país. Un titular de prensa podría decir algo así como «el Partido Famoso gobierna en las comunidades más ricas de España», con lo que sus dirigentes pueden sacar pecho y presumir de apoyos poderosos e influyentes … y a su tesorero le vendrá muy bien pedir un crédito al banco de la esquina. Sin embargo, el dirigente del PF está que se sale, así que cambia el titular a «las comunidades más ricas de España son aquellas donde gobierna el Partido Famoso.» Con lo que envía el mensaje subliminal de que, en cuanto el PF llega a un gobierno, esa comunidad se vuelve rica y próspera. Como ven, basta con cambiar el orden de los factores para que la relación causa-efecto sugiera algo radicalmente distinto.
No se crean que esto se ve solamente en los casos de manipulación política. Incluso estudios serios caen a veces en esta trampa. Uno de los resultados que más me llamaron la atención en la última encuesta PISA (que examina de modo sistemático y a gran escala los resultados escolares de niños en muchos países) fue una relación entre la puntuación media obtenida por los alumnos en lectura y el número de libros que tenían en casa. Ambas cantidades tienden a crecer, o a decrecer, al unísono. El problema viene cuando hay que escoger una causa. En el Informe PISA podemos leer «la puntuación media obtenida por los alumnos en comprensión lectora se ve influida de modo notable por el número de libros en casa. Cuanto mayor es el número de libros que el alumnado tiene en casa, más alta es la puntuación media que obtiene.» Con eso, el informe ya ha concluido que, si tienes más libros en casa, entonces obtendrás mayor nota en lectura.
Pero no se dan motivos, ni el mecanismo en que esas variables se influyen la una a la otra. ¿Cómo se decide qué es lo que causa qué? ¿Por qué no puede ser al revés? Yo puedo imaginarme lo contrario, esto es, que los niños con mayor puntuación lectora son aquellos a los que más gusta la lectura. Cuanto más te gusta leer, más libros pedirás a tus padres (o incluso te los comprarás tú mismo), y en consecuencia, más libros tendrás en casa. La causa es ahora la consecuencia.
Personalmente, creo que tener más libros en casa no sirve de nada si no te los quieres leer. Tener libros en casa es una condición necesaria, no suficiente, para tener buenas notas en lectura. Sin embargo, los encargados de llevar a cabo las políticas educativas toman estos informes y piensan algo así como «si los niños tienen más libros, entonces sacarán mejores notas en lectura; por lo tanto, compremos más libros a los niños» Dicho y hecho, gastan dinero del presupuesto para comprar más libros (o más ordenadores, pizarras digitales, una hora extra de lectura a la semana) … y luego descubren asombrados que el rendimiento escolar no aumenta. Hay muchos motivos, pero uno de ellos puede ser que la relación causa-efecto no ha sido bien entendida.
La inversión de la relación causa-efecto es asimismo un truco de publicidad muy usado. En este momento hay un anuncion que lo ejemplifica al pelo, pero como no quiero líos legales, voy a usar nombres ficticios. Llamemos Romualdinho a nuestro protagonista publicitario: joven, rico, deportista de élite, sale en televisión un día sí y otro también. Un día, lo vemos en un anuncio televisivo diciendo que, como no le gusta perder, tiene su dinero en el Banco Brando. Una voz en off nos dice: «si es usted como Romualdinho, contrate nuestro nuevo Depósito Interesante del Banco Brando.» A => B.
O, lo que es lo mismo, no B => no A: si usted no contrata el Depósito Interesante, entonces es que no es usted como Romualdinho. ¿Y quién no quisiera ser como él? No hacer caso de su «recomendación» implica darle la espalda a todo lo que él representa: éxito, fama, fortuna. Así que sus seguidores, los que «se identifican con él» caen en la trampa lógica, creyendo que usar su banco, su espuma de afeitar y su coche les acerca un poco más a sus valores.
¿Demasiado falaz para que los clientes piquen? No, a juzgar por los anuncios que vemos todos los días. Constantemente nos vemos asediados por famosos de todo tipo que pretenden hacernos creer en la bondad de ciertos productos y servicios poniendo su fama como garantía. Romualdinho tiene su dinero en el Banco Brando. Robert deNiro nos dice que «el carácter no se vende» en un anuncio de whisky. Bertín Osborne tiene claro con qué jamón no se la juega. Todos, de forma más o menos sutil, intentan convencernos de que, si usamos lo que ellos anuncian, entonces seremos un poco más como ellos. Siempre es el mismo esquema. Si quieres ser como yo, entonces compra lo que estos señores dicen.
Claro que incluso este truco solamente puede usarse con moderación, no vaya a ser que los pardillos acaben sospechando. Es aquí donde aparece en escena un truco más sutil y poderoso. Los publicistas desearían que, en este punto, usted dejase de leer. Pero como veo que no está usted por la labor, bien por usted. Se trata de una segunda alternativa a A => B, a saber:
Alternativa 2. C es la causa, y tanto A como B son las consecuencias.
En este esquema, A y B no están relacionados directamente, sino por vía de una tercera causa. Ahora vamos a fijarnos en el tenista Pepe Total, que anuncia un Tontoyota Quiri. Lo conduce por carretera con una sonrisa de felicidad, lo aparca frente a un restaurante de lujo, lleva a rubias esculturales de un lado para otro. La diferencia con el caso de Romualdinho estriba en la sutileza. En lugar de plantearnos una relación clara estilo «si quieres tener una vida como la de Pepe, entonces tienes que comprarte su coche,» el anuncio se limita a presentarnos dos proposiciones:
A: «Pepe Total tiene una vida envidiable: personalidad, dinero, fama, mujeres, etc.»
B: «Pepe Total conduce un Quiri»
… y deja que el espectador saque sus conclusiones. Pero, en el fondo, olvidan el hecho C, que lo origina todo: «Pepe Total es el campeón del mundo de tenis.» Por eso tiene una vida envidiable (ningún problema con eso, se lo ha ganado), y por eso los fabricantes del Tontoyota Quiri lo quieren anunciando su producto. Sin la causa C, los hechos A y B no estarían relacionados en modo alguno. El anunciante ha logrado que el cliente identifique el producto (B) con las cualidades de un hombre respetado (A).
Esta lógica retorcida puede usarse de modo muy perverso. Un conductor misógino podría justificar su actitud hacia las mujeres: «yo no digo nada, PERO cuando las mujeres no conducían las pólizas de seguros eran mucho menos caras» Cuando no existía Internet, las llamadas telefónicas no eran tan caras; cuando las mujeres no votaban, no había guerras mundiales; y antes de que nos obligasen a usar DNI no había armas nucleares. Todo son falacias derivadas de que dos hechos cambien de forma similar por el mero cambio del tiempo.
Eso lo vemos por todos lados. Los políticos ven que cada vez hay más delincuencia, y que cada vez hay más inmigración. Resultado: los inmigrantes son unos delincuentes. La economía iba bien cuando los obreros tenían garantías laborales. Resultado: hay que «flexibilizar» el mercado laboral para volver a los brotes verdes. Hay en este un viejo chiste de científicos. Un biólogo grita a una araña «salta», y ésta salta. Le quita una pata a la araña, vuelve a gritarle y vuelve a saltar. Así hasta que la araña se queda sin patas. El biólogo grita «salta» y la araña no se mueve. La conclusión del sabio es: si les quitas todas las patas, la araña se vuelve sorda.
Podríamos hacer todo tipo de relaciones tontas pero aparentemente lógicas. Mi favorita, que se hizo famosa hace algún tiempo, es una en la que se relaciona la temperatura media de los océanos con el número global de piratas:
De hacer caso literal a esta gráfica, parecería que los piratas tienen una sensibilidad a la temperatura mayor que la de los corales tropicales. No es que los vayamos a echar de menos, pero podría resultar interesante estudiar los mecanismos que llevan a hombre tan rudos y curtidos al borde de la extinción.
Claro que puede que hayamos equivocado los papeles. La desaparición de los piratas puede no ser la consecuencia del aumento de las temperaturas, ¡sino su causa! De algún modo, los piratas mantenían el equilibro térmico del planeta, y su captura está rompiendo dicho equilibrio. Si queremos luchar contra el calentamiento global, tendríamos que dejar de perseguirlos. ¡Ministra, hay que cancelar la Operación Atalanta! Me imagino a Jack Sparrow (perdón: al capitán Jack Sparrow), encerrado en su celda y perorando con sus captores a través de los barrotes: «no, yo no digo nada, pero cuando los piratas dominábamos los siete mares, no hacía este calor tan insoportable.» Menos mal que su tripulación siempre vuelve; aunque a estas alturas me pregunto si será para liberar a su amado capitán o para recuperar el equilibrio climático planetario.
Por supuesto, hay una causa subyacente a ambos fenómenos: el progreso tecnológico. Gracias a él podemos perseguir a los piratas con mayor eficiencia, y debido a él se están calentando los océanos. O podemos buscar las causas en factores socioeconómicos, demográficos o políticos, que cambian con el tiempo.
O vaya usted a saber si hay siquiera relación entre A y B. Lo que nos lleva a la última relación posible entre ambos sucesos:
Alternativa 3: Ninguna de las anteriores
No siempre dos sucesos simultáneos están causados uno por el otro. Si hay alguna relación seria entre el número de piratas y la temperatura media de los océanos, es tan compleja y sutil que será muy difícil encontrarla.
Hace algún tiempo, algo me llamó la atención muy vivamente en un informe que leí sobre el tema («Las diferencias entre países y regiones en las pruebas PISA» por Julio Carabaña, Catedrático de Sociología de la Universidad Cumplutense de Madrid). Por lo visto, el Congreso de EEUU encargó en los años 60 un informe para justificar la intervención del gobierno federal en las escuelas y complementar los fondos en las escuelas más pobres. Cuál no sería su sorpresa cuando el llamado Informe Coleman concluyó que la relación entre los recursos puestos en juego y la mejora en el aprendizaje resultante eran … cero.
Datos más recientes en España nos muestran asimismo un panorama extraño. Analizando los resultados de las diferentes comunidades, no parece haber una relación entre gasto por alumno y resultado académico. En España, se gasta en promedio unos 3.160 euros por alumno, y la puntuación medida por el informe PISA para los alumnos españoles es de 488 puntos. En La Rioja, se gastan casi lo mismo (3.170€ por alumno), y la puntuación de los alumnos riojanos es de 520; por su parte, Castilla y León obtiene la misma puntuación con un gasto de 3.540 euros por enano. El País Vasco se gasta casi 4.800 euros por niño, pero sólo obtienene una puntuación de 495; mucho mejor lo hacen los navarros, cuyos niños alcanzan 510 puntos gastando 4.240 euros por niño. Y los catalanes, a pesar de quedarse un poco detrás de ellos (491 puntos), lo hacen más eficientemente, ya que sólo invierten 2.840 euros por niño.
Estos datos pueden ser mal esgrimidos por personas interesadas en crear polémica interterritorial (seguro que han oído hablar de más de un caso en los telediarios), pero es algo que sucede lo mismo fuera de nuestras fronteras. Los resultados de los niños de Hungría, España y Alemania son casi idénticos, pero los alemanes gastan por alumno el doble que los húngaros y un 50% más que nosotros. Luxemburgo se gasta ocho veces más que Tailandia, para obtener los mismos resultados. Los estrellas en el informe PISA, los surcoreanos, se gastan algo menos por alumno que los griegos, pero obtienen un resultado casi un 20% superior. Y los Estados Unidos empatan en resultados con los checos … después de gastarse más del doble por alumno.
¿Quiere decir que no hay relación entre gasto por alumno y rendimiento académico? La lógica nos dice que debe haberla. Sin dinero no hay buena escuelas, profesores, aulas o libros. Ningún político en su sano juicio puede mirar los datos anteriores y decidir que lo mejor para aumentar el rendimiento escolar es reducir los presupuestos para educación.
Está claro que no existe una explicación sencilla a esta relación gasto-resultados. Diferencias culturales, nivel de vida de las familias, la ley de los rendimientos decrecientes … nada que se pueda arreglar fácilmente con una explicación sencilla. Así que la próxima vez que oigan algo del tipo «se van a dar ordenadores a los alumnos para que mejoren su rendimiento académico» recuerden que, si hay una relación de ese tipo, es tenue y está oculta bajo un millar de otras causas y relaciones, a cual más compleja.
Todo eso suponiendo que exista esa relación. Desde antes de la Edad de Piedra, el ser humano está acostumbrado, casi obsesionado, con buscar causas a los fenómenos que vemos a nuestro alrededor. Es un mecanismo evolutivo lógico. Si estoy en medio de la sabana y noto que los matorrales se mueven, busco enseguida una causa en mi mente. Del resultado puede depender mi propia vida, especialmente si la causa es un tigre al acecho. Pero si calibras mal la causa, puede ser peor el remedio que la enfermedad. «Los sagitario son gente de fiar» puede parecer una creencia inocua … hasta que descubres que el sagitario en quien depositaste tu confianza y tus ahorros se ha fugado al extranjero con tu dinero.
Establecer buenas relaciones causales es una buena inversión en la propia supervivencia. Haga la prueba. En la próxima pausa publicitaria, o en el telediario, fíjese y verá cuántas relaciones causales ficticias encuentra. O limítese a creerme y confiar en mí, cosa que no le recomiendo. A fin de cuentas, todos saben lo falsos que podemos llegar a ser los libra.




Gran artículo, Arturo. Muy bien explicado.
Saludos
Cuando los políticos entran por la puerta la lógica sale por la ventana. Si algo sale bien (PI, empleo) es porque son muy listos y trabajadores. Si la cosa va mal es por culpa del gobierno anterior.
De igual forman razonan (no solo ellos, tambien gran parte de la sociedad) ante problemas como la educación, administación o sanidad: A más dinero mejores servicios y resultados.
No existe tal linealidad al menos de forma constante. El decir que sin dinero no hay escuelas ni hospitales es un sofisma. Obvio. Y sin lanzamientos del shuttle tampoco hay fallos en las juntas.
El problema es que no se analizan otras variables. Se supedita todo el dinero y este factor, a partir de cierta cantidad, ya no es la principal influencia.
Y, con el informe PISA, todos caemos en ese error, igual que en Challenger. Se discute mucho por los fallos y no los éxitos. Casi todos para combatir el fracaso escolar o subir el nivel dan la misma solución: más dinero.
Estamos atascados para la solución de problemas sociales y encima tenemos a las ideologias que se imponen como dogmas.
En cierta manera estamos como estuvo parte de la física durante casi 2000 años. Como ARISTOTELES dijo que la velocidad de caida depende de la masa del cuerpo, nadie osó contradecirle. Era «evidente y lógico» para cualquiera: una pluma tarda más en llegar al suelo que una piedra, ergo la masa tiene la culpa. Tal vez alguno se diera cuenta que una capa hecha un ovillo tarda menos en llegar al suelo que una igual desplegada. Pero como el gran ARI habia dicho que la masa pues la masa, al fin y al cabo los griegos (Euclides, Arquimedes..) eran muy listos y no se equivocaban. Y asi estuvimos hasta que llegó Galileo.
Buen artículo. Tanto que, en mi opinión vale por dos: uno sobre el accidente del Challenger y otro sobre causalidad. Y no sé cuál de ellos me gusta más.
Excelente artículo, me ha encantado. Gracias. Creo que sería mejor usar «juntas tóricas» en lugar de los «anillos O» que queda bastante raro y creo que todos los que las usamos decimos o-rings en inglés o tóricas en español. Es sólo una sugerencia.
Con mis disculpas para los que no sabemos nada de Fisica, nos serviria mucho que uses el mismo ejemplo que es mas didactico para efectos de entender los puntos o hechos expuestos. Gracias por el articulo. Supongo que luego hablas sobre la Correlacion y si hablas de la correlacion de Pearson o la correlacion en si misma. Gracias.