
En el artículo anterior dejamos a nuestra vaca subiendo y bajando en el aire. La cuestión a responder, os recuerdo, era determinar si al lanzarla verticalmente tardaría más, menos o igual en llegar hasta el punto más alto que en bajar hasta llegar al punto de origen.
Estaba implícito en el enunciado un conjunto de simplificaciones. Tuvimos que suponer una fuerza de rozamiento con el aire (llamada viscosidad), pero suponíamos despreciables las influencias debidas a la rotación de la Tierra, efectos cuánticos, relativistas, atracción de otros cuerpos, etc. Por cierto, ya que he mencionado la palabra “despreciable”, sabed que no tiene el mismo significado en ciencia que en el habla cotidiana. Una persona despreciable sería alguien a quien no vamos a invitar a cenar a casa, pero en ciencia un efecto despreciable es algo que podemos despreciar (es decir, descartar) por su minúsculo efecto en el resultado. Por ejemplo, suponemos que la atracción gravitatoria entre el planeta Júpiter y nuestra vaca es despreciable por lo pequeño.
Uno de los efectos que no consideré por despreciable fue el de Arquímedes. En efecto, si nuestra vaca esférica se encuentra viajando por el aire, éste ejercerá una fuerza hacia arriba igual al peso del volumen del fluido (en este caso, aire) desalojado. Puesto que el volumen de una vaca lleno de aire tiene una masa pequeña no lo tuvimos en cuenta, pero en cualquier caso resulta irrelevante. El motivo es este:
 La diferencia ahora consiste en el nuevo término de fuerza de Arquímedes (flecha violeta). Esa fuerza depende del volumen del objeto y de la densidad del fluido que le rodea, además de la aceleración gravitatoria. Seguimos suponiendo que nuestra vaca es esférica (aunque me he permitido ponerle pezuñas y orejas en el dibujo porque queda más mono) y de volumen constante, así que el empuje de Arquímedes es el mismo para la subida que para la bajada. Yo tuve en cuenta ese efecto, y como es el mismo durante la subida que durante la bajada, el resultado no cambia, y sigue tardando algo más en caer que en subir.
La diferencia ahora consiste en el nuevo término de fuerza de Arquímedes (flecha violeta). Esa fuerza depende del volumen del objeto y de la densidad del fluido que le rodea, además de la aceleración gravitatoria. Seguimos suponiendo que nuestra vaca es esférica (aunque me he permitido ponerle pezuñas y orejas en el dibujo porque queda más mono) y de volumen constante, así que el empuje de Arquímedes es el mismo para la subida que para la bajada. Yo tuve en cuenta ese efecto, y como es el mismo durante la subida que durante la bajada, el resultado no cambia, y sigue tardando algo más en caer que en subir.
La fuerza de Arquímedes es el origen de la vieja pregunta-trampa “¿qué pesa más, un kilo de plomo o un kilo de paja?” Se supone que un kilo es un kilo, y por tanto deberían pesar igual; pero como se pesa en el seno de la atmósfera terrestre, la cosa cambia, ya que la paja tiene menor densidad y por tanto mayor volumen que el plomo. Eso quiere decir que el empuje de Arquímedes es mayor para la paja, y puesto que va en sentido opuesto a la gravedad, un kilo de paja pesaría menos que un kilo de plomo. Por supuesto, si hacemos las medidas al vacío ambos objetos “pesan” lo mismo.
Pero al final del post pregunté si la situación sería la misma en el agua. ¿Qué cambia ahora? En términos de fuerza de viscosidad, nada. Para un objeto tanto da el aire como el agua, ya que ambos son fluidos. Vale, sí hay una diferencia: los líquidos se consideran incompresibles (que no se comprimen, no vayan a confundirlos con “incomprensibles”) y los gases no lo son. En ambos casos las fuerzas de viscosidad son del mismo tipo, así que nuestra argumentación anterior no cambia. Este comentario lo explica muy bien, y valdría incluso en el aire, ya que la densidad varía pero depende de la altura, así que a igual altura igual densidad e igual fuerza de Arquímedes.
En términos de la fuerza de Arquímedes, la cosa sí puede cambiar. Imaginemos que nuestra vaca esférica se hunde con el Titanic. En el momento del impacto contra el fondo del océano, la vaca recibe un empujón inicial hacia arriba. Si la vaca es más densa que el agua, la situación será idéntica que en el aire, y de nuevo todo será igual que antes: tardará un cierto tiempo en subir hasta una altura máxima, y luego algo más de tiempo en volver abajo.
Pero atención, porque si la vaca es menos densa que el agua la cosa cambia. En este caso la fuerza de Arquímedes superará a la gravitatoria; la vaca se limitará a subir a la superficie del mar y quedarse allí flotando a la espera del Carpathia. En tal caso desaparece la suposición inicial del problema (que la vaca subirá y luego bajará) y la situación es diferente.
Para aprovechar los últimos minutos de clase, vamos a reformular el problema de la vaca esférica menos densa que el aire. El Titanic está a punto de irse a pique, así que nuestra vaca se lanza desde lo alto del barco, cae al agua y se hunde. Como es menos densa que el aire, flotará. La pregunta ahora es: ¿tardará más, menos o igual en hundirse hasta una profundidad máxima que en volver a flote?
La situación sería algo así:
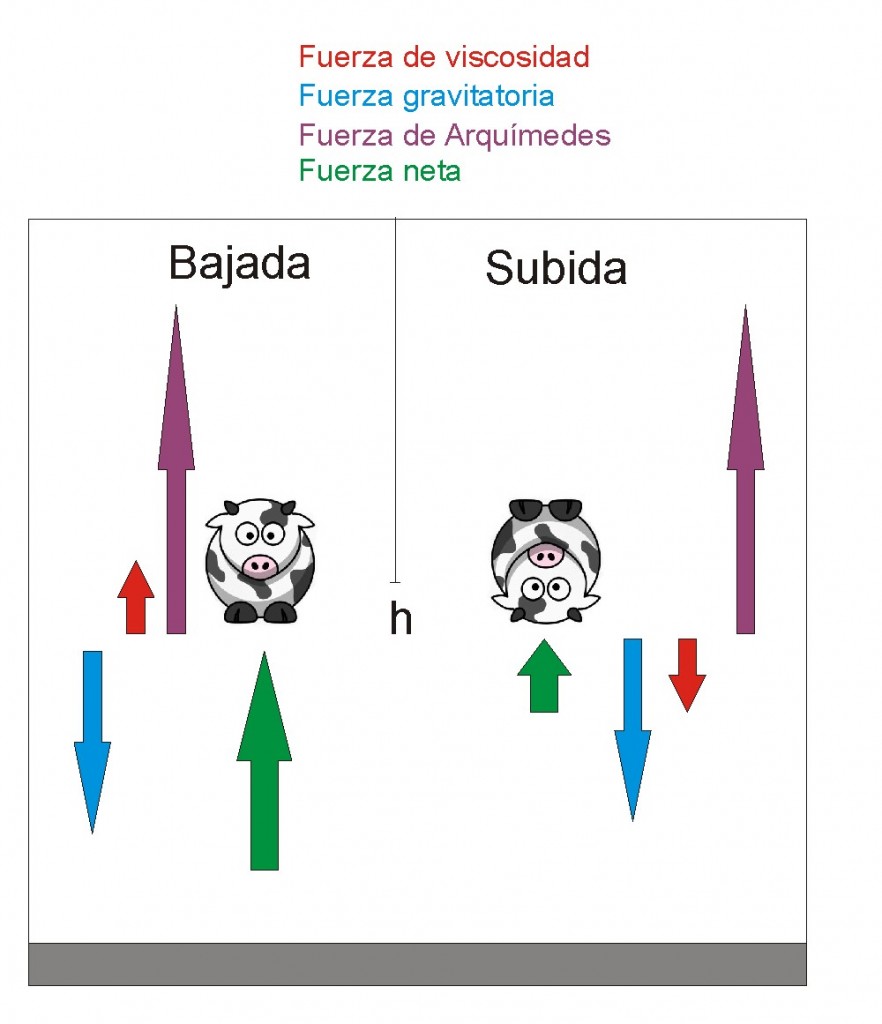 En este caso la fuerza neta (flecha verde) ha cambiado de sentido y apunta hacia arriba, pero podemos hacer las mismas consideraciones que en el caso anterior. Durante la subida la fuerza neta sobre la vaca es mayor que durante la bajada, por tanto alcanzará mayor velocidad en cada punto de la caída, por tanto la vaca tardará menos tiempo en caer hasta una profundidad máxima que en volver a subir a la superficie del agua.
En este caso la fuerza neta (flecha verde) ha cambiado de sentido y apunta hacia arriba, pero podemos hacer las mismas consideraciones que en el caso anterior. Durante la subida la fuerza neta sobre la vaca es mayor que durante la bajada, por tanto alcanzará mayor velocidad en cada punto de la caída, por tanto la vaca tardará menos tiempo en caer hasta una profundidad máxima que en volver a subir a la superficie del agua.
Recordemos que el caso de la vaca cayendo en el aire, con viscosidad, era el objeto de la pregunta del anterior post. Entonces concluimos que la bajada tardaba más que la subida. Ahora aparentemente es lo contrario, puesto que la subida tarda más que la bajada.
Pero en realidad, la diferencia no es tal porque “subida” y “bajada” representa dos fases distintas del movimiento para ambos casos. Cuando la vaca está en el aire, primero sube y luego basa; en el agua primero baja y luego sube. Si olvidamos los términos subida y bajada, y en su lugar nos fijamos en el viaje de ida y el de vuelta, podemos comparar ambos casos (ascensión en el aire y hundimiento en el agua):
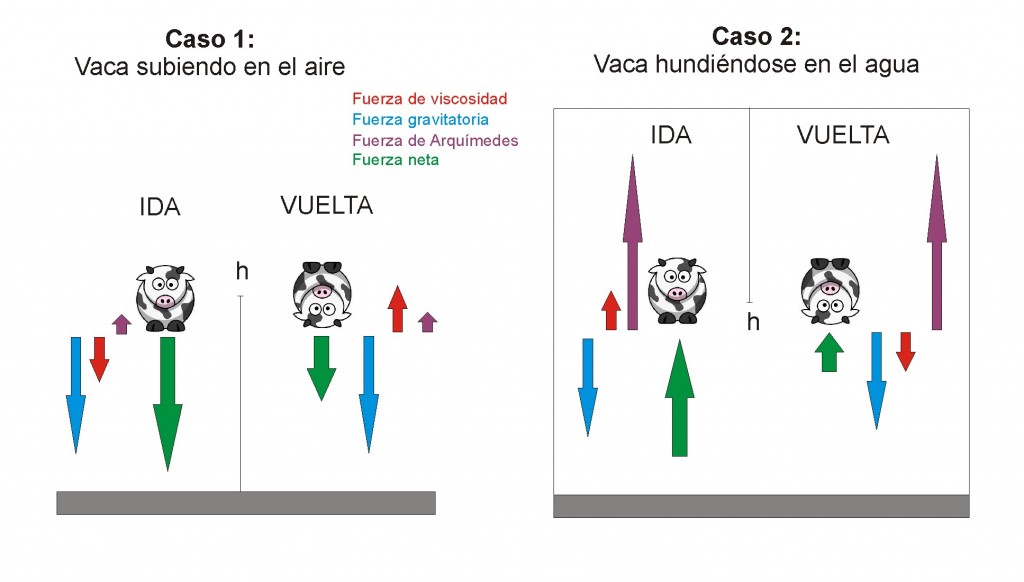 Ahora vemos más claro que, tanto en un caso como en el otro, la fuerza neta sobre la vaca (en valor absoluto, sin preocuparnos por el signo) es mayor durante la ida que durante la vuelta. Así pues, y a pesar de que ambas situaciones parecen muy diferentes, el resultado es el mismo: se tarda más en el trayecto de vuelta que en el de ida.
Ahora vemos más claro que, tanto en un caso como en el otro, la fuerza neta sobre la vaca (en valor absoluto, sin preocuparnos por el signo) es mayor durante la ida que durante la vuelta. Así pues, y a pesar de que ambas situaciones parecen muy diferentes, el resultado es el mismo: se tarda más en el trayecto de vuelta que en el de ida.
Que ambas situaciones son más similares de lo que parece en un principio puede verse con algo más de claridad si cambiamos nuestro sistema de referencia. Ahora vamos a suponer que vemos el caso 2 (vaca hundiéndose en el agua) pero nos ponemos cabeza abajo. En ese caso cambiamos el arriba y el abajo, y este es el resultado:
 Fíjese el lector en los dos casos durante la ida. En ambos casos la fuerza de viscosidad apunta hacia abajo. De las dos fuerzas restantes (gravedad y Arquímedes), la mayor apunta hacia abajo. Durante la vuelta tenemos que la viscosidad apunta hacia arriba, y de las dos restantes (gravedad y Arquímedes) la mayor apunta nuevamente hacia abajo.
Fíjese el lector en los dos casos durante la ida. En ambos casos la fuerza de viscosidad apunta hacia abajo. De las dos fuerzas restantes (gravedad y Arquímedes), la mayor apunta hacia abajo. Durante la vuelta tenemos que la viscosidad apunta hacia arriba, y de las dos restantes (gravedad y Arquímedes) la mayor apunta nuevamente hacia abajo.
Resultado: en ambos casos la fuerza neta apunta hacia abajo tanto en la ida como en la vuelta, pero en la ida la magnitud de la fuerza neta es mayor, con lo que la velocidad aumentará más rápidamente, con lo que el tiempo de ida será menor que el de vuelta. O dicho de otro modo: el viaje de ida tarda más que el viaje de vuelta.
Vale, ahora hagámoslo por energías. En el caso de que la… RIIIIIIING….. vaya, ha sonado el timbre, así que lo dejaremos aquí por hoy. Hasta la semana que viene.


Me sorprende mucho que este magnifico articulo, que creo aclara los puntos oscuros que nos quedaron en el anterior no despierte ningun interes.
Espero que sea porque, como a mi, me ha aclarado lo que no veia tan evidente en el anterior y no tengo nada que añadir.
Espero con impaciencia la tercera entrega profesor.
La verdad es que para los que no somos físicos, un camino intermedio entre la física de colegio y los estados cuanticos de los decabit es de agradecer.
Un saludo.
Hola, hace unas semanas apareció pegado en la puerta de mi casa el dibujo de lo que yo identifiqué como una vaca esférica… resulta que mi hijo le dio por pintar un gato un tanto especial.
Evidentemente el equivocado era yo, ya que estaba predispuesto a ver vacas esféricas después de leer tu artículo.
Si hubiera sido una vaca te aseguro que la hubiera escaneado y enviado para goce y disfrute de todos.
Un saludo
el tiempo de ida será menor que el de vuelta. O dicho de otro modo: el viaje de ida tarda más que el viaje de vuelta.