
El otro día recibí una consulta por Twitter acerca de un problema de Física. Era tan sencillo que cabía en un solo tuit, y al mismo tiempo tan completo que me decidí a escribir este post.
Primero, el problema:
Me gustó es su sencillez, y al mismo tiempo su riqueza de matices. Se trata de uno de esos problemas que han de resolverse conceptualmente, es decir, nada de “sustituyo en esta ecuación y sale la respuesta.” No es un problema en concreto donde nos den los parámetros relevantes, escogemos la ecuación adecuada, sustituimos y recuadramos el resultado con Boli rojo.
Vamos a resolverlo. Para ello, si no les importa, voy a hacer algo que a los científicos nos critican mucho: simplificar. Muchas veces nos acusan de reduccionistas, como si fuese algo malo, pero lo cierto es que reducir un problema complicado a uno sencillo es un primer paso válido y más sencillo. Ya sabemos que las vacas esféricas en el vacío no existen pero por algo hay que empezar, así que resolvemos el problema básico y luego le vamos añadiendo complicaciones: el aire, los cuernos, las manchas negras, el certificado de Sanidad, etc.
Este problema, en su vertiente sencilla (sin viscosidad con el aire), se puede resolver por dinámica (leyes de Newton) o por energías. Escojo lo segundo. La idea es que la energía mecánica (potencial más cinética) se conserva si no hay otras fuerzas que disipen energía de otras formas. Vamos a imaginar un cuerpo en dos momentos de su trayectoria: cuando sube y cuando baja. En ambos casos, se encuentra a la misma altura, a la que llamaré h: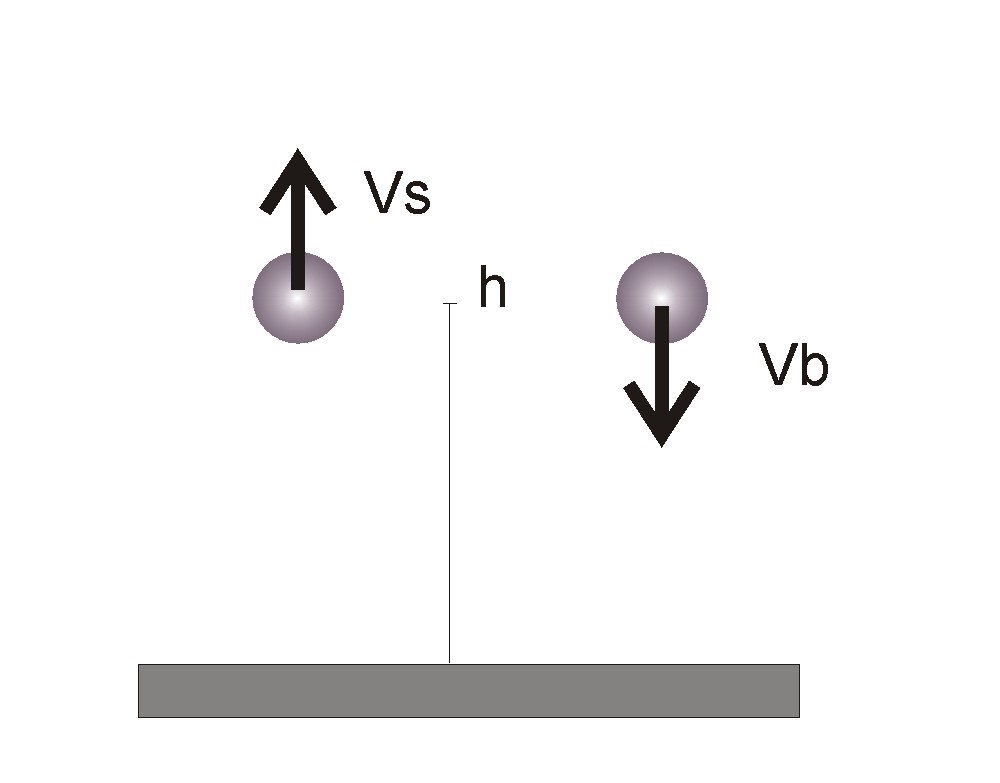 (En realidad, ambas bolas deberían estar sobre la vertical, pero las separo horizontalmente para que se vea mejor. El desplazamiento horizontal es irrelevante para la resolución de nuestro problema)
(En realidad, ambas bolas deberían estar sobre la vertical, pero las separo horizontalmente para que se vea mejor. El desplazamiento horizontal es irrelevante para la resolución de nuestro problema)
La bola en subida tiene una energía que es suma de dos términos: energía potencial gravitatoria mgh+C y energía cinética ½mVs2. De modo análogo para el caso de bajada: mgh+C + ½mVb2
Quizá le sorprenda ese término “+ C” que aparecen en el término potencial. No debería, ya que la energía potencial se define salvo una constante. Habitualmente se escoge la constante C=0, que es la más sencilla, pero nunca hay que olvidar que no existe obligación y que podemos darle a C el valor que nos dé la gana, con tal de que sea siempre el mismo. No importa porque que lo que nos interesa es la diferencia de energía. Igualando la energía a la subida y a la bajada tenemos:
mgh + C + ½mVs2 = mgh+C + ½mVb2
de donde sale que Vb = ± Vs. En este caso tenemos dos soluciones matemáticas, y llega el momento de determinar si alguna de ellas es una solución física. Ya sabemos que ambos vectores velocidad tienen signos opuestos (si uno apunta hacia arriba, el otro apunta hacia abajo), por lo que la solución que nos interesa es la Vb = – Vs. En cualquier caso, esto nos dice que la velocidad (en módulo) es el mismo en la subida que en la bajada, y eso para cualquier altura h. Conclusión: el movimiento de subida y el de bajada son idénticos (de hecho, uno se convierte en el otro si damos marcha atrás en el tiempo), y por tanto recorren la misma distancia en el mismo tiempo.
Se puede ver también aplicando la segunda ley de Newton, y en realidad sería preferible haberlo hecho así, ya que aparecerá la dependencia explícita de la posición con el tiempo. No lo he hecho porque la herramienta de trabajar por energías nos permite resolver el problema que tenemos pendiente, donde aparecen fuerzas de viscosidad debidas al aire. Esas fuerzas no son constantes, y resulta muy difícil usar la ecuación habitual F=ma, ya que la fuerza de viscosidad depende de la velocidad, que depende de la aceleración, que depende de la fuerza, que depende de la velocidad… y ya tenemos la pescadilla que se mueve la cola. Habría que resolverlo por métodos numéricos, y la solución sería complicada además de aproximada.
Pero por energía la cosa se resuelve fácilmente. Para entenderlo, supongamos que hay fuerza de viscosidad debido al movimiento en el seno del aire. Ahora la energía mecánica (suma de cinética y potencial) ya no se conserva, puesto que una parte se ha transmitido al aire y se ha convertido en movimiento del aire, calor, sonido y en general cosas que no influyen en el movimiento. Bien, llamemos W a esa energía perdida. Ahora la ecuación del balance energético quedaría así:
mgh + C + ½mVs2 = mgh+C + ½mVb2 + W
Despejando un poquito nos queda que Vs2 = Vb2 + 2W/m, y puesto que W es una cantidad positiva tenemos que │Vs│ > │Vb│, donde a partir de ahora hablaré del módulo de las velocidades, que es lo que importa. Esto significa que, en cualquier altura h, la velocidad de bajada es menor que la de subida, y por tanto el tiempo de bajada será mayor que el de subida. Así pues, la respuesta será: la bola tarda más en volver al punto de origen que en subir al punto más alto.
Fíjense en la elegancia del planteamiento. No sabemos cuál es la altura máxima, ni la velocidad inicial, ni la aceleración de la gravedad, ni el diámetro de la bola, ¡ni falta que hace! Basta con consideraciones generales basadas en el principio de conservación de la energía.
Leí un hilo en Twitter con una discusión basada en las fuerzas, no en las energías. Había quien decía que el problema de subida y el de bajada son simétricos, y por tanto ambos tiempos deberían ser iguales. Eso es algo que estamos acostumbrados a ver en el caso sin viscosidad del aire, pero como el caso con viscosidad no suele verse (salvo en fluidos, y no siempre) nos quedamos sin saber el final de la película. De acuerdo, es la hora de los spoilers: la situación no es simétrica.
Para ello hay que tener en cuenta una particularidad de las fuerzas de viscosidad: al contrario que otras fuerzas (como la gravitatoria), no siempre tiene el mismo valor para un objeto sino que depende de la velocidad de éste. Y no sólo depende en módulo sino también en signo: se opone al movimiento. Si usted quiere mover el sillón hacia la derecha tendrá que vencer la fuerza de rozamiento que actúa hacia la izquierda, y si quiere moverlo hacia la izquierda, el rozamiento actuará hacia la derecha.
Una gráfica y veamos cómo la situación no es simétrica:
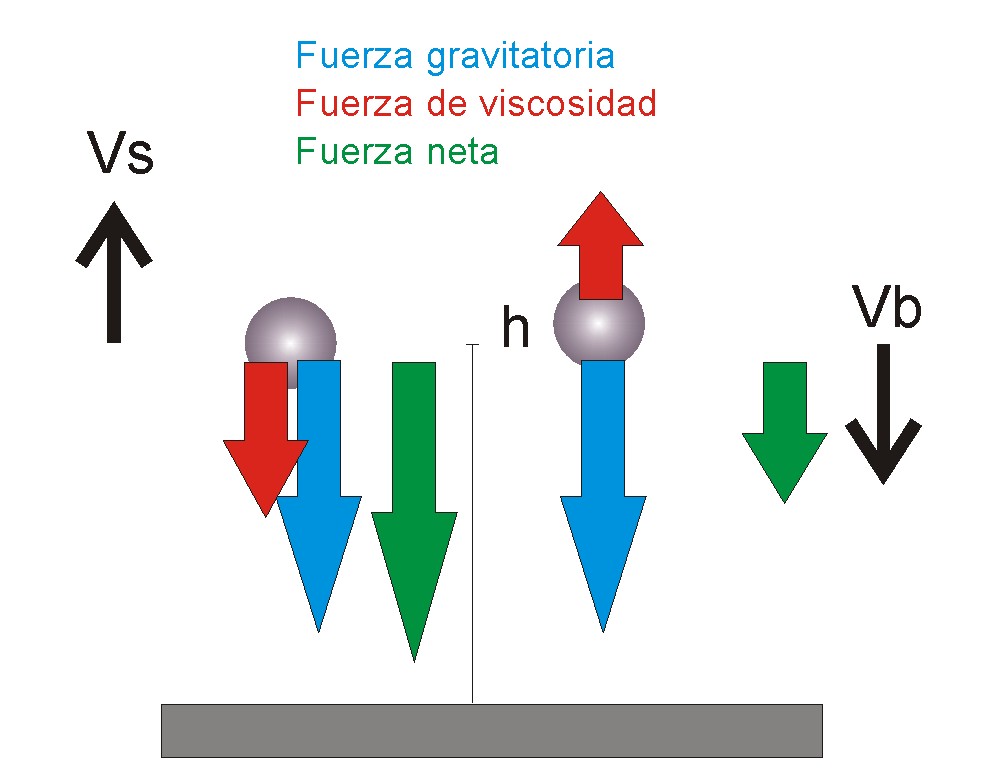 Lo primero que hay que reseñar es que la fuerza de viscosidad depende de la velocidad, por lo que su valor absoluto en subida y en bajada (flechas rojas) no tiene por qué ser el mismo. Pero no importa. El detalle fundamental es que, durante la subida, la viscosidad se suma a la fuerza gravitatoria, y durante la bajada se resta. Por tanto, en cualquier punto h el valor absoluto de la fuerza total (flecha verde) es mayor durante la subida que durante la bajada. Lo que queda es un razonamiento análogo al de antes: si durante la bajada la aceleración siempre es menor, la velocidad aumenta más lentamente, y por tanto tardará más tiempo en recorrer la misma distancia. Nuevamente la bola tarda más en caer al punto de origen que en subir al punto más alto.
Lo primero que hay que reseñar es que la fuerza de viscosidad depende de la velocidad, por lo que su valor absoluto en subida y en bajada (flechas rojas) no tiene por qué ser el mismo. Pero no importa. El detalle fundamental es que, durante la subida, la viscosidad se suma a la fuerza gravitatoria, y durante la bajada se resta. Por tanto, en cualquier punto h el valor absoluto de la fuerza total (flecha verde) es mayor durante la subida que durante la bajada. Lo que queda es un razonamiento análogo al de antes: si durante la bajada la aceleración siempre es menor, la velocidad aumenta más lentamente, y por tanto tardará más tiempo en recorrer la misma distancia. Nuevamente la bola tarda más en caer al punto de origen que en subir al punto más alto.
De ese modo, y por dos métodos diferentes, hemos demostrado que la vaca esférica tarda lo mismo en subir que en bajar en el vacío, pero no en un medio viscoso como el aire. Estrictamente hablando tendríamos que considerar también el empuje de Arquímedes ejercido por el aire sobre la vaca, pero el resultado no cambiaría. Ahora bien, ¿qué pasaría en el agua? ¿Pasaría lo mismo si la vaca fuese más densa que el agua? Y si fuese menos densa, ¿tardaría el mismo tiempo en hundirse a una profundidad D que en volver a la superficie? ¿Mas? ¿Menos?
Eso, amigos, lo dejo como ejercicio al lector. Pero quiero respuesta razonada o no le pondré nota.


Lo cierto es que es bastante intuitivo si se conoce que como la gravitatoria es una fuerza conservativa lo único que importa es el rozamiento en su caída para ver que sus velocidades no son iguales. Respecto a lo último, mi razonamiento es el siguiente:
Si fuese más densa que el agua, en la subida se opondría a: la fuerza gravitatoria, al rozamiento y le ayudaría el propio empujón del agua, que ocuparía su lugar, disminuyendo de energía potencial y dándole energía cinética al objeto. La fuerza de la presión se compensaría por ser igual en ambos lados. En la caída, estaría en contra del rozamiento, Fr, y además se opondría el propio agua que desplaza, Fag, pero tendría a su favor la fuerza gravitatoria, Fg. Al ser más denso, significa que la fuerza gravitatoria del objeto es mayor que la debida al agua que desplaza Fg>Fag. En ambos casos, la fuerza de rozamiento se opone al movimiento, solo que durante la bajada esta se suma a Fag y en el ascenso, a Fg. Aún así, como salvo por Fr son todas fuerzas conservativas, la energía mecánica cuando está en su pico en la subida es la misma que durante el momento inicial de su bajada, por lo que solamente tenemos que contar Fr, que le resta energía cinética en su descenso, concluyendo que baja más lento,
Por otro lado: de ser menos denso, al hundirse, se le opondría con mayor fuerza el agua que desplaza que su propia fuerza debida a la gravedad, junto con el propio rozamiento. Alcanzada una profundidad h, donde su velocidad es cero, vuelve hacia arriba, esta vez con la fuerza de rozamiento hacia abajo, entorpeciendo su ascenso y haciendo que tarde más en subir que en bajar, ya que merma la energía cinética que consigue del empujón hacia arriba, y la energía mecánica que tiene al inicio de su ascenso y al final de su descenso es la misma
Como el empuje del agua es constante (suponiendo que el agua es un fluido incompresible) se puede aplicar el mismo razonamiento, tardara mas en subir a la superficie que en hundirse.
Y si es mas denso que el agua, pues no flotara y se hundira hasta el fondo.
En el caso de que el cuerpo estuviera sumergido en el agua se tendrían que tener en cuenta tres fuerzas: la de la gravedad (P), la fuerza de rozamiento (Fr) y la ocasionada por la fuerza de Arquímedes (H). La fuerza P es constante siempre (en pequeñas distancias, claro), la fuerza Fr es contraria a la dirección de la velocidad y proporcional al cuadrado de la misma, y la fuerza H es constante y contraria al peso (igual al peso del fluido desalojado por el cuerpo). Por tanto, en el caso de que la densidad sea mayor que el agua, la resultante de la suma de P+H va a ser de la dirección de P, con lo que al tener en cuenta la Fr la suma de las fuerzas va a ser mayor cuando suba el cuerpo ya que Fr ira en la misma dirección que P+H, que cuando baje que ira en la dirección opuesta a P+H. Por lo tanto tardará menos en subir que en bajar.
Pero cuando la densidad sea menor, la suma de P+H será de la dirección de H y pasará justo lo contrario por lo que la resultante de las fuerzas será mayor en la bajada que en la subida, y en este caso, tardará menos en bajar que en subir. En este segundo caso será necesario por tanto que el impulso inicial sea para abajo y no hacia arriba, ya que sino no se podría comparar el proceso de la subida con el de la bajada.
Saludos.
Indudablemente, la capacidad didactica del profesor es enorme.
Pero quisiera hacer una pequeña puntualización, usted diferencia entre agüa y aire, dado que es muy dificil encontrar una «vaca esferica» más ligera que este, pero profesor, agüa y aire son fluidos y por tanto en ambos casos habría que considerar el arquimedes de toda la vida.
Aunque claro, en el caso del aire u otros fluidos muy poco densos, la flotabilidad o fuerza ejercida por el fluido para expulsar el cuerpo, puede ser tan pequeña que sea desdpreciables, ¡pero existe en todo fluido!
¿Que pasa si la esfera es hueca y está llena de helio de tal forma que la masa atraida por la gravedad es casi nula — no nula —? Evidentemente nada. Para su analisis es irrelevante, ascenderia y caeria, punto. Por lentamente que se desarrollara el experimento.
Pero la consideración hecha con un fluido denso como el agüa seria igüalmente aplicable al aire. ¿no es cierto?
Por otro lado, el señor Lennart hace una puntualizacion interesante en este sentido.
¿Afectaria al experimento si el fluido es comprensible o no?
Tal como yo lo veo, es un cuerpo moviendose a traves de un conjunto de moléculas, así pues, tal consideracion solamente afectaria a la viscosidad y por tanto a la fricción, pero no al moviemiento en si, supongo.
Saludos.
Un detaille, esa fuerza de flotacion solo aparece si en el fluido hay un gradiente de presion, que aparece cuando este esta sujeto a una aceleracion, como el de la gravedad. Si el fluido estuvira flotando en el espacio, o en caida libre, no habria ninguna flotacion. 🙂
Un saludo
Cierto, aunque creo que no hemos planteado que suceda en esas codiciones.
En todo caso. Cuando dice usted caida libre supongo que se refiere a una situación de micro gravedad como la existente en el vacio — el espacio -..
Entiendo que la vaca esferica, cuando alcanza el cenit y comienza a caer solamente está influida por la aceleración de la gravedad, es decir, cae libremente. Si no fuera así, no caeria.
(Tampoco se dentendría, seguiria en movimiento, ¿no es cierto?)
Aunque nos la cojemos con papel de fumar, ya que en realidad, todo objeto está siempre en caida libre, una orbita es caida libre y un objeto en el vacio del espacio siempre esta «callendo» hacia una atracción gravitacional.
Por tanto, siempre hay una cierta aceleración. Por despreciabel que sea.
Por cierto, ¿me equivoco al pensar que si calculamos la atracción entre dos cuerpos cualquiera, el valor nunca es nulo?
Si por caida libre nos referimso a un sistema libre de influencia externa, entonces estamos hablando de otra cosa.
Y que conste que es mas pregunta de estudiante que opinion, mi fisica esta bastente olvidada y solamente aprendi la necesaria para ingeniería, asi que…
Efectivamente, existe una fuerza de arquimedes. Pero, si la densidad del fluido no varia, como puede ocurrir cuando la diferencia de altura es pequeña, esta fuerza sera constante, y por tanto el razonamiento anterior es aplicable. Habria que tener en cuenta la suma de las dos fuerzas.
Si el fluido es compresible, la densidad variaria dependiendo de la altura. Si las propiedades del fluido dependen solamente de la altura y son constantes, podemos aplicar el mismo razonamiento, ya que seria una fuerza conservativa. Si añadimos un termino de la energia debido a la fuerza de flotacion, f(h), que depende solo de la altura, y igualamos la energia a la subida y a la bajada:
mgh + C + ½mVs2 + f(h) = mgh+C + ½mVb2 + W + f(h)
Como antes, podemos quitar mgh y C, ademas de f(h), ya que a la misma altura sera igual:
½mVs2 = ½mVb2 + W
Vs2 = Vb2 + 2W/m
Por tanto llegamos a la misma expresion, la velocidad en la subida siempre sera mayor, y tardara menos en subir que en volver.
Muy interesante el articulo por cierto.
Gracias por aclararlo.
Entonces, si no lo entiendo mal, el factor no es considerar distintos los fluidos a los que se aplica de igüal manera, sino si son o no comprensibles y como afecta la interaccion molecular al cuerpo.
Interesante.
Estaba acostumbrado a considerar la densidad de los fluidos y si son o no comprensibles, pero no habia considerado este aspecto.
Estos problemas me gusta resolverlos llevándolos al extremo.
Si lanzo la bola hacia arriba a 1 km/s, va a subir a gran velocidad hasta que se pare. Pero en la bajada alcanzará la velocidad terminal, mucho menor que 1 km/s y a partir de ahí no varía. Por tanto baja más despacio y tarda más.
Gracias. En tres líneas y todo claro.
¿Por qué la fuerza de rozamiento (que genera calor, viento y sonido) es mayor al bajar que al subir si las moléculas del aire que se oponen al movimiento son casi iguales?
Respuesta en una palabra : BÁDMINTON
Un post muy interesante, pero me queda una duda… Cuando haces el balance energético e introduces W, por qué lo haces solo en la bajada? En la subida también hay pérdidas de energía en todas las formas que describes.
Muchas gracias.
Durante la subida, parte de la energía de la lleva el aire. Si, pero a nosotros lo que nos interesa es que la altura alcanzada es la que determina la energía potencial con la que contamos para la bajada. Es menor con aire que en el vacío, pero eso no importa. Lo que importa es que durante la baja, esa nueva y menor energía, es la que vuelve a convertirse en energía cinética más una nueva pérdida, una nueva W.
No obstante, habría que tener en cuenta (solo a efectos del cálculo de tiempos y alturas concretas), que el valor de la viscosidad también de pende de la presión atmosférica que varía continuamente con la altura y la temperatura.