«¿Cómo es posible que este montón de metal pueda sustentarse en el aire?» Esa pregunta nos la hemos hecho muchas veces, y aun hoy el ciudadano medio tiende a aceptarlo como artículo de fe. Hay muchas explicaciones en Internet, pero algunas son confusas, otras están equivocadas y otras más nos dejan como estábamos; y reitero lo que ya he dicho en Twitter, «Brujería» no vale.
No es porque no haya habido buenas mentes y plumas (vale, teclados) ocupados en esa tarea. Hace un par de años, la Pizarrade Yuri (desactualizada ahora, por desgracia) nos regaló la vista con una estupenda explicación. También se hicieron eco del problema en Microsiervos, en enchufa2 y en la muy recomendable web de Malaciencia (aquí y aquí); por no hablar del siempre excelente Francis, a quien no me atrevo yo a contradecir a la ligera.
El problema es que no tengo más remedio que intentarlo. Francis metió el dedo en la llaga con su afirmación de que los libros de texto se equivocan. Como profe de Física, ya he visto antes casos en los que la realidad no es tal y como la cuentan en algunos libros de texto. Cada vez tenemos más ejemplos: el caso del microondas, el del Puente de Tacoma Narrows (y su primo español), la fuerza de Coriolis, y otros más. Ahora puede que tenga que tachar otro ejemplo de mi lista. El caso es que me he puesto a bucear en busca de información, y he vuelto a la superficie cargado de caracolas interesantes.
La explicación tradicional se basa en el principio de Bernoulli. Este señor tan listo enunció hace ya muchos años la relación existente entre los diversos parámetros de un fluido, a saber: la presión P, la velocidad v, la densidad ρ y su altura h:
P + ρgh + ½ρv2 = constante
donde g es la aceleración de la gravedad; es la llamada ecuación de Bernoulli. La explicación clásica pasa porque el ala de un avión está diseñada de forma que el aire tenga que recorrer una distancia mayor en la parte superior del ala; de esa forma, su velocidad será más alta, su presión disminuirá, y el efecto será una diferencia de presión que empuja al avión hacia arriba. Esa es la que se suele denominar «explicación Bernoulli.» Hay una variante, llamada «explicación Venturi,» similar a la anterior: el aire se acelera en el extradós igual que lo haría en un tubo que sufre un estrechamiento. En realidad, considero que ambas explicaciones son equivalentes, ya que ambas están basadas en la misma ecuación, de modo que a efectos prácticos las tomaré como la misma.
Ninguna de estas explicaciones se considera válida. Tomaré el razonamiento de Yuri, que se explica la mar de bien. Contra la explicación Venturi, afirma que el extradós de un ala (la parte superior) no es una boquilla de Venturi. En contra de la explicación Bernoulli, afirma que la sustentación es muy inferior a la necesaria para levantar el avión; yo no he hecho los cálculos, pero voy a admitir este punto. En ambos casos se aduce también el problema del vuelo invertido: si la explicación Venturi/Bernoulli fuese cierta, ¿cómo podría un avión volar boca abajo? No suelen hacerlo, pero todos hemos visto videos de exhibición donde cazas a reacción o avionetas cruzan el cielo de forma invertida.
Una tercera explicación, que podríamos llamar «explicación Newton» sugiere que el aire, al golpear el ala por abajo, la empuja hacia arriba. Para verla en acción, no hay más que sacar la mano cuando vamos de pasajero en un coche. Ponedla horizontal, y no notaréis gran cosa; inclinadla un poco hacia arriba y veréis cómo la mano tiende a subir como el F-14 de Maverick. Paradójicamente, Yuri niega la explicación Newton afirmando que también hay aire en la parte superior. En efecto, la hay, pero no golpea el ala (o la mano) con la misma fuerza que el aire de la parte inferior, así que no podemos descartar esta explicación. Por otro lado, cuando la superficie del ala está horizontal, la explicación Newton no funciona, y en ese caso habrá que buscar otra cosa.
Finalmente (no porque no haya más, sino por no resultar cansino), una cuarta explicación se basa en el hecho de que el aire es un fluido viscoso, lo que hace que se pegue a la superficie del ala. La fuerza de atracción entre ala y aire empuja a éste hacia abajo, y por tanto eleva a aquélla. Es el llamado efecto Coandă, lo que nos permite bautizarla como «explicación Coandă.»
El problema es que ninguna de esas explicaciones es válida por sí sola, y cualquier intento por explicar el vuelo del avión en términos de «esto y no lo otro» se encontrará con dificultades. Alf, de Malaciencia, se lió un poco justamente por eso. Escribió un primer artículo abogando por la explicación Newton, y al día siguiente se decantó por una mezcla de Newton y Coandă, con un leve toque de Bernoulli, para acabar diciéndonos que no importa, porque Newton y Bernoulli son equivalentes. Como ven, incluso entre los mejores hay confusión.
Lo que es peor, ninguna de las explicaciones resuelve la cuestión de por qué un avión puede volar invertido. El punto filipino aquí es que cualquiera de los mecanismos anteriores que pudiese explicar el vuelo de un avión cuando va «cabeza arriba» invertirá de signo el efecto y tenderá a arrojarlo en picado cuando vuele «cabeza abajo.»
Es en este momento cuando el profe saca los bártulos. Por si os pica la curiosidad y no podéis esperar al final, os adelanto que la explicación correcta es… no, mejor paso de spoilers. Leed y aprended. Qué malo soy.
Comencemos con los dibujitos. En todas las explicaciones sobre la sustentación alar se introduce el corte de un ala, y esta no será una excepción. He aquí la sección aproximada de un ala típica (hay muchas), lo que veríamos desde el lateral del avión si Chuck Norris llegase y le diese un golpe de kárate al ala en la dirección longitudinal de la nave (de proa a popa):
El ala se mueve de derecha a izquierda, pero como lo importante es el movimiento relativo resulta más cómodo suponer que el ala está quieta y es el aire el que se mueve proveniente de la izquierda; es lo que se hace en los túneles de viento, por ejemplo. Sea como sea, el aire choca con la zona delantera del ala (el llamado borde de ataque) y se divide en dos flujos, superior e inferior. Las zonas superior e inferior del ala se denominan extradós e intradós, respectivamente. Finalmente, hay un parámetro muy importante, que mide el ángulo formado por el ala y la horizontal, llamado ángulo de ataque. En lo que sigue, vamos a suponer un ángulo de ataque pequeño. Hay otros parámetros de interés para calcular de modo detallado la sustentación de un ala, pero no entraremos en ellos.
Muy bien, comencemos. El aire se pone en marcha, y dos moléculas de aire (A y B) chocan con el borde de ataque. Una de ellas pasa por encima del ala y la otra por debajo. Cuando hayan pasado el ala, ambas moléculas volverán a encontrarse. Si seguimos el convenio de suponer ala fija y aire en movimiento, esta sería la trayectoria de ambas moléculas:
De ese modo, la molécula A ha recorrido una distancia superior. Si suponemos que no hay turbulencias, la ecuación de Bernoulli entra en acción y nos dice que la presión en el extradós es inferior a la presión en el intradós. Esta diferencia de presiones resulta en una fuerza neta hacia arriba. Cuando el avión haya carreteado y obtenido velocidad suficiente, la fuerza neta conseguirá superar el peso del avión, y allá vamos, hacia la inmensidad del cielo azul.
Bonita explicación. El problema es que es incorrecta. Para comenzar, he de confesar que les he mentido por omisión. La ecuación de Bernoulli arriba indicada es válida solamente en caso de un fluido ideal, en el que no haya fuerzas de rozamiento interno ni interacciones con otros objetos como la propia ala. Si tenemos un fluido ideal no hay sustentación por Bernoulli, y el flujo de aire será algo parecido a esto:
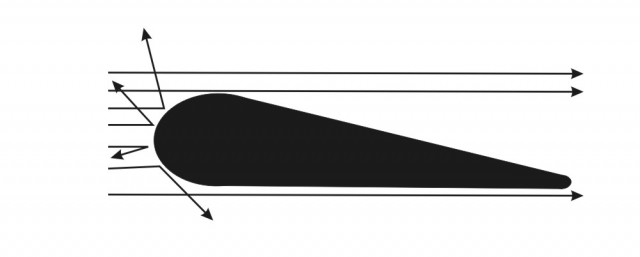 Como ven, las moléculas de aire chocan con el borde de ataque del ala y rebotan como si fuesen un puñado de canicas, pero ahora el flujo no se curva en el extradós siguiendo la superficie del ala. Para que eso suceda, necesitamos un mecanismo interno que ligue las moléculas de aire entre ellas para permitir una interacción entre las capas de aire, y en este caso no lo tenemos.
Como ven, las moléculas de aire chocan con el borde de ataque del ala y rebotan como si fuesen un puñado de canicas, pero ahora el flujo no se curva en el extradós siguiendo la superficie del ala. Para que eso suceda, necesitamos un mecanismo interno que ligue las moléculas de aire entre ellas para permitir una interacción entre las capas de aire, y en este caso no lo tenemos.
En un fluido real, debemos tener en cuenta el rozamiento interno, que recibe el nombre de viscosidad. Es un término que tiene relación con la facilidad o dificultad para que un líquido o un gas fluya. Un fluido muy viscoso fluirá con gran dificultad, como la mantequilla o el petróleo, en tanto que gases o líquidos poco viscosos como el alcohol fluirán con pocos impedimentos. ¿Recordáis los anuncios de la chica del futuro que nos trae la lejía? Se echa un pegote en la mano, lo mueve con un dedo y dice eso de «mira qué densa es,» como dando a entender que está cuajada de sustancias limpiadoras. En realidad debió haber dicho «mira qué viscosa es,» pero claro, a ver quién vende eso con semejante eslogan.
Imaginaos ahora que el aire que fluye por el extradós, por encima del ala, es como un conjunto de láminas que se deslizan unas sobre otras. Podéis hacer el experimento en casa: tomad un paquete de folios, poned encima la mano abierta, y movedla en la dirección paralela a la mesa. Veréis que el folio que estáis tocando se mueve mucho, los de más abajo se mueven menos, y el folio que está en contacto con la mesa no se ha movido. Cuando no hay turbulencia, las capas de aire se mueven así, como su fuesen láminas que se deslizan unas sobre otras; por eso se denomina régimen laminar.
Eso es bueno, porque ahora sí podemos dibujar bien las líneas de corriente alrededor del ala. La lámina de aire más cercana al ala no se mueve (es la llamada capa límite), y arrastra consigo a la lámina siguiente, que a su vez mueve la lámina adyacente, y así sucesivamente. El movimiento sería algo parecido a esto: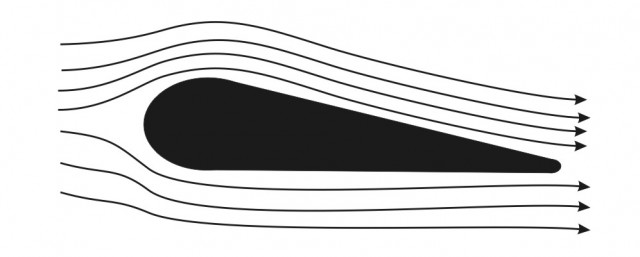 Ahora comenzamos a llegar a alguna parte. La viscosidad fuerza a las capas de aire a seguir el perfil de ala, y el efecto Bernoulli proporciona sustentación. Todavía tenemos que explicar dos fallos del presente razonamiento. Primero: la sustentación debida a Bernoulli (o a Venturi, que no nos vamos a pelear por eso) es numéricamente insuficiente para levantar un avión. Segundo: seguimos sin saber cómo diablos puede volar un avión de forma invertida.
Ahora comenzamos a llegar a alguna parte. La viscosidad fuerza a las capas de aire a seguir el perfil de ala, y el efecto Bernoulli proporciona sustentación. Todavía tenemos que explicar dos fallos del presente razonamiento. Primero: la sustentación debida a Bernoulli (o a Venturi, que no nos vamos a pelear por eso) es numéricamente insuficiente para levantar un avión. Segundo: seguimos sin saber cómo diablos puede volar un avión de forma invertida.
Hay un efecto que incrementa la sustentación: la tercera ley de Newton, o ley de acción y reacción. Esta ley dice que si tú empujas algo en una dirección, ese algo te empuja a tí en sentido opuesto. Empujamos agua hacia atrás y nadamos; empujamos el suelo con tus zapatos y caminamos; empujamos aire caliente hacia abajo y el cohete despega. Bien, pues fíjense de nuevo en el movimiento del aire al pasar por el extradós: Conforme pasa el ala del avión, lanza grandes masas de aire hacia abajo (fenómeno conocido con el nombre de downwash). Como resultado, esas masas de aire empujan al ala hacia arriba. Así de sencillo. En este caso, la curvatura alar en el extradós no solamente produce la sustentación por el efecto Bernoulli sino también por el efecto de acción y reacción, un doble efecto combinado Newton+Bernoulli. En cierto modo, recuerda la explicación Newton tradicional, pero con una diferencia: no es la masa de aire del intradós la que provoca la sustentación, sino la del extradós. El aire tira del ala hacia arriba en lugar de empujarle desde abajo.
Conforme pasa el ala del avión, lanza grandes masas de aire hacia abajo (fenómeno conocido con el nombre de downwash). Como resultado, esas masas de aire empujan al ala hacia arriba. Así de sencillo. En este caso, la curvatura alar en el extradós no solamente produce la sustentación por el efecto Bernoulli sino también por el efecto de acción y reacción, un doble efecto combinado Newton+Bernoulli. En cierto modo, recuerda la explicación Newton tradicional, pero con una diferencia: no es la masa de aire del intradós la que provoca la sustentación, sino la del extradós. El aire tira del ala hacia arriba en lugar de empujarle desde abajo.
Seguimos sin poder explicar cómo puede volar un avión boca abajo, así que algo falta. La explicación rigurosa exigiría echar mano de las ecuaciones de Navier-Stokes, auténtica artillería pesada que me niego a explicarles aquí (quiero que sigamos siendo amigos). Incluso aplicar la ecuación de Bernoulli en forma diferencial para una trayectoria curva se hace cuesta arriba, así que voy a limitarme a una descripción somera, sin ecuaciones.
Imaginemos una fina lámina de aire que se curva sobre la superficie del extradós. Para curvarla, hace falta una fuerza centrípeta. Esa fuerza implica una diferencia de presiones, y el resultado es que la cara inferior de la lámina de aire, la que está tocando el ala, tiene una presión ligeramente menor que la cara superior. Conforme nos alejamos del ala, las láminas de aire van teniendo valores de presión cada vez mayor, hasta que nos alejemos lo suficiente, caso en que la presión será la atmosférica. El resultado es que la presión en el extradós es menor que la atmosférica. En la otra cara del ala, la del intradós, sucede justamente lo contrario. Consecuencia: una diferencia de presión que sustenta el ala.
Esta explicación, que voy a llamar «explicación de Bernoulli CTQS (Como Tiene Que Ser)» recuerda levemente a la explicación tradicional: el movimiento de aire provoca una diferencia de presiones entre el intradós y el extradós, cuyo resultado es una fuerza neta de sustentación. Pero hay una diferencia fundamental: no hemos usado para nada la idea habitual de «el aire recorre mayor distancia por la parte superior que por la inferior.» Eso significa que incluso un ala de sección simétrica podría generar sustentación en determinadas condiciones.
Hay un detalle adicional que no he mencionado y que ahora puede ser explicado. ¿Recuerdan lo que les conté antes sobre las moléculas A y B, las que circulan por el extradós y el intradós, respectivamente? Se supone que ambas llegan al extremo del ala en el mismo instante. En la práctica, no es así: al reducirse la presión en el extradós, se acelera el aire, y la molécula A llega a la meta antes incluso quela B, a pesar de haber recorrido una distancia mayor: Este es el tipo de efectos que el esquema Bernoulli tradicional era incapaz de explicar. En realidad, la ecuación de Bernoulli es tan sólo una aproximación, basada en el principio de conservación de la energía mecánica. Con viscosidad de por medio, el fluido pierde o gana energía extra por rozamiento tanto con las demás capas como con la propia superficie del ala.
Este es el tipo de efectos que el esquema Bernoulli tradicional era incapaz de explicar. En realidad, la ecuación de Bernoulli es tan sólo una aproximación, basada en el principio de conservación de la energía mecánica. Con viscosidad de por medio, el fluido pierde o gana energía extra por rozamiento tanto con las demás capas como con la propia superficie del ala.
Por fin vamos a poder responder a la pregunta de «¿cómo diablos vuela un avión en posición invertida?» Entra ahora en juego un parámetro que no hemos considerado hasta ahora: el ángulo de ataque. Como a estas alturas vamos sobrados, veámoslo con un ala de sección simétrica:
Con ángulo de ataque cero, el movimiento del aire por el intradós sería igual que por el extradós, y por tanto no tendríamos sustentación ni por Bernoulli ni por Newton. Pero inclinemos un poco el ángulo que forma el ala con la horizontal:
Como ven, las líneas de flujo de aire que hay a la derecha tienden hacia abajo (efecto Newton), y las de debajo del ala están menos juntas (efecto Bernoulli). Tenemos una señora sustentación como está mandado.
Ahora hagamos la pirueta Maverick para volar al revés. Es fácil. No hay más que poner el ala con un ángulo de ataque negativo, que nos daría una sustentación negativa:
y acto seguido girar el avión 180º para ponerlo boca abajo. Ahora la sustentación negativa se convierte en positiva. ¡Tachán! Por supuesto, otra cosa es que la estructura del avión aguante, así que no intente hacerlo en un avión de pasajeros. Denzel Washington lo hizo recientemente, pero se trataba de una película. Por lo que he leído en foros de aviación, es dudoso que un avión comercial de pasajeros pudiera siquiera intentarlo. Dejaré este punto a los aerotrastornados expertos.
Un pequeño detalle que debe que tener en cuenta todo aprendiz a entrar en Top Gun es que lo dicho hasta ahora es solamente válido para ángulos de ataque inferiores a un valor determinado. Si el ala se inclina más aún, su capa límite de aire se despegará y se acabó la sustentación. El avión entrará en pérdida y mas valdrá tener a mano la palanca del asiento eyector:
- Imagen: Holger Babinski
Lo más interesante de la explicación «Bernoulli CTQS» es que nos permite jugar con otros tipos de perfiles alares. Hasta ahora hemos jugado con perfiles plano-convexos o biconvexos. Fíjense lo que sucede cuando el intradós tiene forma cóncava:
Las curvaturas de ambas superficies se combinan para dar una diferencia de presiones aún más alta que en los ejemplos anteriores, así como un flujo de aire saliendo en dirección hacia la derecha y hacia abajo. Este perfil proporciona una gran sustentación, y muchas aves se aprovechan de ello. Para que vean que esto funciona también con aviones, fíjense en la siguiente imagen, extraída del artículo de Anderson y Eberhardt. Se trata del Curtis modelo D tipo IV, el segundo avión adquirido por el ejército de EEUU, allá por 1911. El intradós y el extradós tienen la misma longitud, y sin embargo este bicho volaba.

Como conclusión, y para zanjar la polémica de una vez por todas: la explicación correcta es… todas las anteriores. Como ese viejo cuento en el que un grupo de ciegos palpa un elefante y cada uno siente un animal diferente, nosotros hemos estado viendo un problema desde diversos ángulos, y cada uno hemos llegado a una conclusión correcta, lógica… pero parcial. A partir de ahora, los profes de Física tendremos que dejar bien claro en el aula que la explicación Bernoulli contribuye, pero no se basta sola. Los diversos efectos que hemos visto en este artículo cooperan en la tarea común:
– Las capas de aire alrededor del ala se van curvando suavemente, produciendo una zona de baja presión en el extradós (explicación Venturi/Bernoulli)
– La curvatura de las láminas de aire se producen por la viscosidad del aire y la existencia de una capa límite (explicación Coandă)
– El aire saliente lleva una dirección inclinada hacia abajo, produciendo una fuerza hacia arriba en el ala (explicación Newton)
Y aquí paz y después gloria.
Referencias:
– Holger Babinksy, How do wings work? (PDF). Physics Education 38, 497-503 (2003)
– Holger Babinsky, How do wings work? Smoke streamlines around an airfoil (Video) Youtube, cuenta Francis WorldInsideOut
– David Anderson, Scott Eberhardt, A physical revision of flight; revisited (PDF)
– Así vuela un aviónLa Pizarra de Yuri
– ¿Por qué vuela un avión? Microsiervos
– Unos apuntes sobre «así vuela un avión» Enchufa2
– Bernoulli no explica por qué vuelan los aviones (o sobre la circulación alrededor de un ala y cómo los libros de texto a veces se equivocan) Francis (th)E mule Science´s News
– ¿Por qué vuela un avión? Malaciencia, 14/9/2005







Genial. Hasta ahora nunca había conseguido enterarme.. y lo había intentado.
Por fin podré dormir traquilo 😉
Genial el post.
Hasta ahora la explicacion que me habia parecido mas informada es la que dan en «Understanding Flight», escrito por un piloto y fisico (CERN y Los Alamos), y un doctor en aeronautica por la Universidad de Washington e ingeniero de Boeing. Es un libro tecnico en cuanto a lo que trata, pero de divulgacion, no tiene matematicas.
Ellos tambien invalidan la aplicacion del principio de Bernoulli y efecto Venturi en un apendice, y basan el peso del argumento en la tercera ley de Newton y el downwash. Explican que la forma del ala contribuye a su eficiencia y caracteristicas de entrada en perdida, pero es fundamentalmente irrelevante para explicar la sustentacion, donde segun ellos lo primoridial es el angulo de ataque y el downwash (hay alas con muchos perfiles y formas, en particular las hay finas como el papel de fumar en cazas).
El downwash es tambien lo que hace que los flaps incrementen tanto la sustentacion, divierten un monton de aire hacia abajo.
Pero ya te digo que lo explican a nivel divulgativo, tu has podido ver numericamente si la contribucion de Newton es notoriamente superior a la del resto de fenomenos?
Perdón por el «troleo», pero soy químico y la explicación más plausible que se me ocurre es que los aviones vuelan gracias a la Química… Es decir, gracias a la reacción química de combustión que hace que los propulsores hagan correr al avión a toda pastilla. Luego sí, Bernoulli y lo que quieras, pero si el avión está parado se cae. Los cohetes y misiles bien que vuelan y no tienen alas. Las alas y todo eso, pues para el «ajuste fino», y en los aviones sobre todo para aterrizar sanos y salvos. No sé si es impresión mía, pero a mí me da la sensación de que cuánto más rápido es capaz de ir el «bicho», menos alas les ponen…
Un saludo.
si esta bien pero necesito una explicacion de esta pregunta la orientación del ala de un avión con respecto al flujo de aire hace que la velocidad del aire encima del ala sea mayor que la velocidad del aire por debajo de esta. Explica en términos de la presión por que se origina una fuerza de sustentación hacia arriba