Hubo un ministro durante la transición (no recuerdo su nombre, lo siento) al que apodaron el sastre porque, cada vez que los periodistas le planteaban un problema, respondía «voy a tomar medidas al respecto.» Ese apodo le vendría muy bien a más de un ministro (o presidente) actual, tan enfrascados en dar tijeretazos y recortes a la economía española. Ya se sabrán ustedes la cantinela: vamos a recortar para volver a la senda del crecimiento, reducir deuda para que nuestra economía despegue, generar confianza en los mercados, ya basta de comer chuches por encima de nuestras posibilidades, etcétera.
Recientemente nos hemos enterado de que quizá todas esas políticas de tijeretazo estén basadas en un error de una hoja de cálculo Excel. Intrigado por el artículo de Naukas donde se han hecho eco de la noticia, y puesto que me quedaron muchas preguntas sin respuesta, me puse a escarbar, y he aquí lo que encontré. Voy a intentar, en la medida de lo posible, dejar a un lado la economía y la política para centrarme en la matemática del dilema; pero no les prometo nada.
EL ESTUDIO DE LA POLÉMICA
En 2010, los economistas Carmen Rinnhart y Kenneth Rogoff publicaron un artículo titulado Growth in a time of debt (Crecimiento en tiempos de crisis), que pronto se convirtió en uno de los más influyentes en su género. Postula la tesis de que, cuando la relación deuda/PIB supera el umbral del 90%, las consecuencias se vuelven catastróficas, provocando una brusca caída del PIB. Las políticas de contención de deuda actuales se basan en esta tesis: por ejemplo, de las siete Previsiones Marco publicadas por la Comisión Europea entre 2010 y 2013, seis citan el estudio de Reinhart y Rogoff (a partir de ahora, «estudio RR») o su umbral del 90%
¿El problema? Un reciente estudio de Thomas Herndon, Michael Ash y Robert Polling («estudio HAP»), del Instituto de Investigación en Política Económica de la Universidad de Massachusetts-Arherst, desdice muchas de las conclusiones del estudio RR y encuentra múltiples irregularidades en los datos manejados por RR.
Me he leído ambos artículos, y también he examinado los datos, que felizmente están disponibles para nuestro disfrute. Mi impresión personal es que los errores de RR no parecen deliberados, sino una mezcla de fallos más o menos chapuceros. Si hay intencionalidad, la han disimulado muy bien; o muy mal, porque deberían haber sido más sutiles. Por mi parte, no tengo motivos para dudar de la honradez de los autores RR.
El problema es que, cuando los errores se corrigen, aparece un panorama radicalmente opuesto al esperado. Sin ánimo de ser exhaustivo, voy a mostrar algunos de los problemas más agudos del estudio RR. Póngase cómodo y pase las palomitas, porque vamos a comenzar por la Tierra Media.
LA MALDICIÓN NEOZELANDESA
El error de Nueva Zelanda ha llamado especialmente la atención. Por algún motivo desconocido, pero que imaginaremos como error inocente, en el estudio RR no se incluyeron los datos correspondientes a ese país para los años 1946-1949. La verdad, olvidarse los datos de cuatro años de posguerra para un país pequeño en las antípodas de Europa no parece algo significativo. Pero lo es, y para eso tenemos que ver cómo RR procesó los datos.
El procedimiento que siguieron es este. En primer lugar, tomaron todos los valores anuales correspondientes al crecimiento (variación anual del PIB) de cada país para cada año, y los dividieron en cuatro bloques en función de las tasas de deuda/PIB: 0-30%, de 30-60%, de 60-90% y más de 90%. Para estimar las contribuciones de cada país a cada uno de esos bloques, tomaron sus datos anuales y los promediaron. De ese modo, aunque un país salga un solo año en el bloque de 0-30% y cincuenta veces en el bloque de 60-90%, ambas contribuciones se contabilizan como equivalentes.
Vale, no se ha enterado de nada, así que voy a simplificarlo con un ejemplo. Bienvenidos, señoras y señores, al Festival de la Canción de Oceaniavisión. Los 61 miembros del jurado deben escoger entre los cuatro países finalistas (Nueva Zelanda, Australia, Japón y Chile), y cada uno de los jurados puede otorgar entre 1 y 12 puntos.
Comienzan las votaciones. Los jurados se decantan de esta forma: 6 votos para Nueva Zelanda, 33 para Australia, 17 para Japón y 5 para Chile. En apariencia, parece que Australia está ganando, pero ojo, porque todavía no sabemos qué puntuación le van a dar a cada uno. Al final, digamos que los puntos se reparten de esta forma: 19 para Nueva Zelanda, 96 para Australia, 66 para Japón y 13 para Chile. La distancia entre nipones y canguros se reduce, pero el resultado final no cambia.
Esto sería lo lógico, ¿no? Pero supongamos que la empresa R&R, patrocinadores de la gala, cambian las reglas de puntuación: ahora los puntos no se suman, sino que se promedian, y el país con mayor promedio ganará el festival. El resultado final es el siguiente: ¡Resultado sorpresa! ¡Japón gana el concurso! Los indignados australianos, ganadores en votos y en puntos, claman al cielo por el pucherazo, los patrocinadores se encogen de hombros, y los japoneses hacen mil reverencias a su cantante por la honorable victoria conseguida mientras los chilenos celebran su paso a la segunda posición.
¡Resultado sorpresa! ¡Japón gana el concurso! Los indignados australianos, ganadores en votos y en puntos, claman al cielo por el pucherazo, los patrocinadores se encogen de hombros, y los japoneses hacen mil reverencias a su cantante por la honorable victoria conseguida mientras los chilenos celebran su paso a la segunda posición.
¿A que suena algo injusto? Bueno, pues resulta que en el estudio RR sucede algo parecido. De hecho, para el ejemplo anterior he tomado los mismos datos que tiene Nueva Zelanda, sólo que en esta ocasión los puntos corresponden al incremento del PIB anual. Resulta que, en 6 años de un total de 61, Nueva Zelanda tuvo una tasa deuda/PIB inferior al 30%; tuvo 33 años con una tasa del 30-60%; 7 años con tasa del 60-90%; y cinco años con tasa superior al 90%.
Sin embargo, Nueva Zelanda no va a contribuir a los datos de forma proporcional al número de años (6-33-17-5), sino al valor medio del crecimiento del PIB de esos años (3,17%, 2,91%, 3,88% y 3,4%). Cincuenta años de deuda moderada apenas pesan más que cinco con deuda elevada. El estudio HAP denomina diplomáticamente «método de pesado poco convencional» a tan original forma de hacer las cuentas, y pide a los autores RR que justifiquen su arbitraria metodología. Deberían, ciertamente.
Pero la cosa puede ponerse aún más fea. Imaginen que cuatro de los cinco jurados partidarios de los chilenos son secuestrados por la mafia canguro. Chile solamente hubiera tenido un votante; pero, oh casualidad, ese votante les entrega nada menos que 12 puntos. Eso le otorga a Chile un total de 12/1 puntos promediados, lo que les hubiera dado la victoria por goleada.
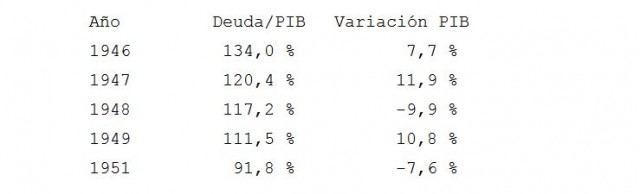
Injusto de toda injusticia, ¿verdad? ¡Pues eso es justamente lo que sucedió en el estudio RR! Bueno, lo de la mafia canguro no (que yo sepa); pero por un error inexplicable, cuatro años dejaron de ser contabilizados, los de 1946-1949. Resulta que cuatro de esos cinco años corresponden a valores de deuda/PIB superiores al 90%; el otro año fue 1951. Fíjense en los datos:
(No aparece 1950 por un pelo, ya que ese año el valor deuda/PIB fue del 87,7%). Si se hubieran tenido en cuenta los cinco años en conjunto, obtendríamos una variación promedio del PIB del 2,6% en el bloque de deuda alta; pero como solamente se consideró el año 1951, resulta que la variación del PIB con el que contribuyó Nueva Zelanda era del -7,6% Ese fallo lastró los resultados finales. Cualquiera que sostenga la tesis de «más deuda implica mayor caída del PIB» hubiera tenido aquí un caso de libro; salvo que no se trata de un ejemplo de libro sino de un error matemático.
¿MEDIA O MEDIANA?
El estudio RR incluye los datos medios sobre la variación del PIB de 20 países avanzados desde 1946 a 2009. El primer problema lo tenemos en el propio estudio, ya que los valores se dan en forma de tabla y de gráfica, y los datos no coinciden: Ignoro el motivo de la discrepancia, y me limitaré a dar por buenos los datos de la Tabla, como hacen en el estudio HAP. A primera vista, parece haber una tendencia a la baja: comenzamos en el 4,1%, que baja a 2,8 hasta que la tasa de deuda supera el 90%, y justo entonces pega un bajón catastrófico. Queda claro que hay un umbral en torno a ese 90%, lo que nos envía un fuerte mensaje: si pasas de este nivel de deuda, vas al abismo de cabeza.
Ignoro el motivo de la discrepancia, y me limitaré a dar por buenos los datos de la Tabla, como hacen en el estudio HAP. A primera vista, parece haber una tendencia a la baja: comenzamos en el 4,1%, que baja a 2,8 hasta que la tasa de deuda supera el 90%, y justo entonces pega un bajón catastrófico. Queda claro que hay un umbral en torno a ese 90%, lo que nos envía un fuerte mensaje: si pasas de este nivel de deuda, vas al abismo de cabeza.
La media aritmética, sin embargo, tiene ciertos problemillas como estimación de un promedio: es bastante sensible a la dispersión de las medidas, no todos los valores contribuyen de la misma manera, y si agrupamos los datos en intervalos el valor medio dependerá de cómo hemos realizado esa agrupamos. Es decir, si los intervalos de deuda/PIB fuesen sido distintos, los valores medios podrían variar sensiblemente. Por otro lado, si un país tiene un valor extremo de crecimiento, repercutirá de forma sensible en la media, como quedó patente tras descubrir el fallo de los datos de Nueva Zelanda.
Por estos motivos, la media suele complementarse con un valor llamado mediana. Para calcular la mediana, ordenamos los datos de menor a mayor, y el valor del dato que esté a mitad de la lista es la mediana. Es decir, si tenemos datos N1, N2, N3, N4, N5, el valor central (N3) es la mediana. La mediana no es tan sensible a las oscilaciones de los datos, y le da cierta estabilidad a la medida, por así decirlo.
Podríamos decir que, si la media y la mediana están cercanas entre sí, los datos están distribuidos de manera uniforme, sin sobresaltos ni valores extremos. Como ilustración, imaginemos a un banquero honrado y trabajador llamado Emilio (¡he dicho imaginemos!), a quien su buen hacer le ha valido un sueldo de 1.000.000€ al mes. Si lo ponemos junto a cien mileuristas, el salario mediano sería de 1.000€, pero el salario medio sería de 10.891€. Ahora id a decirle a un mileurista que 10.891 es un salario representativo, a ver qué cara os pone.
En general hay que tener cuidado cuando la media y la mediana divergen, porque podemos encontrarnos con datos «rebeldes» cuyo promedio no necesariamente es representativo. En el caso del estudio RR, fijaos lo que nos encontramos: Como puede verse, en los tres primeros tramos la diferencia entre media y mediana es pequeña, pero en el de mayor deuda encontramos una fuerte discrepancia: 1,6% para la mediana, -0,1% para la media. Esto huele a que puede haber un Emilio distorsionando los datos. Y en efecto, hay algunos Emilios ocultos en los datos de alta deuda. El principal es, como ya hemos mencionado, el caso de Nueva Zelanda, que influye fuertemente en el resultado final, pero no es el único, ya que no se incluyeron datos de posguerra sobre países como Australia o Canadá. Más aún: había cinco países cuyos datos no se habían tenido en cuenta. El hecho de que sean los primeros en orden alfabético en inglés (Australia, Austria, Bélgica, Canadá, Dinamarca) hace pensar que se trató de un error inocente de copypasteo, pero ahí está, y precisamente el fallo vuelve a afectar al tramo de alta deuda.
Como puede verse, en los tres primeros tramos la diferencia entre media y mediana es pequeña, pero en el de mayor deuda encontramos una fuerte discrepancia: 1,6% para la mediana, -0,1% para la media. Esto huele a que puede haber un Emilio distorsionando los datos. Y en efecto, hay algunos Emilios ocultos en los datos de alta deuda. El principal es, como ya hemos mencionado, el caso de Nueva Zelanda, que influye fuertemente en el resultado final, pero no es el único, ya que no se incluyeron datos de posguerra sobre países como Australia o Canadá. Más aún: había cinco países cuyos datos no se habían tenido en cuenta. El hecho de que sean los primeros en orden alfabético en inglés (Australia, Austria, Bélgica, Canadá, Dinamarca) hace pensar que se trató de un error inocente de copypasteo, pero ahí está, y precisamente el fallo vuelve a afectar al tramo de alta deuda.
Todos cometemos errores, evidentemente, y yo sigo sin creer en una conspiración (demasiado chapuceros); pero si los señores RR se hubieran parado a reflexionar por qué la media y la mediana son tan distintas en el último tramo de deuda/PIB, tal vez hubieran revisado y corregido los datos. Los autores HAP lo hicieron y compararon sus datos corregidos con los originales. He aquí el resultado de las medias:
Bien, lector, ¿había tendencias en los datos originales del estudio RR? ¿Las hay en los datos corregidos del estudio HAP? Pudiera parecer que sí en primera aproximación: leyendo de izquierda a derecha nos encontramos con un dato alto al principio, dos datos intermedios, y luego uno final más bajo. El problema es que matemáticamente no está tan claro, ya que en ningún caso los puntos conforman una línea recta.
Los estadísticos resuelven estos problemas haciendo lo que se llama un ajuste lineal. Eso significa que se calcula la recta que se aproxima más a un conjunto de puntos; entendiendo como «mejor ajuste» no que la recta pase por algún punto en particular, sino que la distancia entre la recta y los puntos arroje una cantidad mínima. Es práctica estándar en estadística, y aunque podamos usar cualquier curva en este caso vamos a restringirnos a rectas.
Pero que podamos calcular una recta para ver la tendencia no significa que los puntos realmente se distribuyan en forma de recta. Para evaluar eso, hay una cantidad llamada coeficiente de correlación lineal (r). Cuando |r|=1, los puntos forman una recta perfecta, y cuanto más bajo sea el valor absoluto de r, tanto peor es ese ajuste. Por lo general, un ajuste con sólo cuatro puntos exigirá un valor de |r| de por lo menos 0,95; menos de eso es un «no sé, parece que, pero no juraría yo que…» Valores más bajos nos harían pensar en el caso del tipo que pone un pie sobre una estufa y otro pie sobre un bloque de hielo para estar cómodo en promedio.
Bien, vamos a ajustar. Las siguientes gráficas corresponden a los datos RR y HAP, junto con las respectivas rectas de mejor ajuste. Los cuatro valores en el eje horizontal (1, 2, 3, 4) indica los cuatro conjuntos de deuda: 0-30%, etc, etc; los del eje vertical indican los valores medios del incremento del PIB:
En ambos casos, los valores de r son negativos, lo que indica que la recta de ajuste tiende hacia abajo. Lo importante es el valor absoluto. Los datos originales RR tenían un valor absoluto del coeficiente r de 0,84. lo que significaría la expulsión a patadas de mi laboratorio de prácticas. La versión modificada HAP es algo más decente, |r|=0,93, lo que no es para tirar cohetes pero entra dentro de lo admisible.
Una diferencia importante es que, si bien ambas gráficas tienen una tendencia a decrecer, la de la derecha lo hace de forma más suave. En ambos casos, el hecho de que haya tan pocos datos hace que la tendencia ser bastante precaria. La recta RR tiene una pendiente de -1,21 con un error de ± 1,49; en el caso HAP, tenemos una pendiente de -0,59 ± 0,45. Es decir, parece que tiende a decrecer, pero no deberíamos poner la mano en el fuego.
Como ven, la información que podemos extraer de un conjunto de cuatro puntos es limitada. ¿Por qué no vamos a la fuente original y extraemos los valores de crecimiento y deuda para todos los años de todos los países industrializados? Quizá eso nos aclare las cosas; y en efecto, lo hace. Pero lo dejaremos para la segunda parte, que no quiero cansarles. Hora del recreo.
Este artículo tiene una segunda parte que puedes encontrar aquí.





Muchas gracias por el exhaustivo análisis, Arturo. La diferencia real en las medias de posguerra no proviene de ningún error, sino de la ponderación de las medias, que es una cuestión de elección conceptual. Además, las medias de posguerra no es más que uno de los 6 análisis en que se basa RR, que de hecho hacen más hincapié en la mediana que en la media.
La exclusión de la posguerra de la IIGM de Australia (1946-1950), Nueva Zelanda (1946-1949), y Canadá (1946-1950) se corrigió en Reinhart, Carmen M., Vincent R. Reinhart, and Kenneth S. Rogoff. 2012. “Public Debt Overhangs: Advanced-Economy Episodes since 1800.” Journal of Economic Perspectives, 26(3): 69-86 (http://www.aeaweb.org/articles.php?doi=10.1257/jep.26.3.69), y las conclusiones eran las mismas.
Según HAP, el error de Excel que excluía a 5 países (Australia, Austria, Bélgica, Canadá y Dinamarca), tenía un impacto marginal en el tramo superior al 90% (pág. 7: http://www.peri.umass.edu/fileadmin/pdf/working_papers/working_papers_301-350/WP322.pdf):
«This spreadsheet error, compounded with other errors, is responsible for a −0.3 percentage- point error in RR’s published average real GDP growth in the highest public debt/GDP category.»
Es decir, pasaría de -0’1 a 0,2. Para llegar al 2,2 que obtienen HAP, tienen que aplicar la ponderación alternativa de las medias propuesta por HAP. James Hamilton cree que las ponderaciones son una cuestión de concepto y piensa que la de RR tiene más sentido:
«One view one could take is that the expected growth rate when a country has a high debt level is a single number across all countries, that is, you expect the real growth rate for Greece when its debt is 90% to be exactly the same number as the real growth rate expected for the U.S. when its debt is 90%. If you further believed that the variance of Greek growth around this mean is the same as the variance of U.S. growth around this mean, then the correct thing to do would be to act as if you have 19 observations on the number of interest from Greece and 4 observations from the U.S., and take a simple average of those 23 numbers. In other words, you should base most of your inference on the data from Greece, because that is where you have the most observations. This is the approach that Herndon, Ash, and Pollin insist is the correct one to use.
Another view you could take is that the expected growth rates for the U.S. and Greece would be different even if the two countries had the same debt levels. From that perspective, there is a different expected growth rate for each particular country when it gets to the 90% debt level, and our goal is to estimate what that number is for a typical country. That view seems to underlie the method chosen by Reinhart and Rogoff, which was to estimate an average growth rate when debt is greater than 90% for the U.S., a separate average growth rate when debt is greater than 90% for Greece, and then take the average of those averages across different countries.»
http://www.econbrowser.com/archives/2013/04/reinhartrogoff.html
«The issue instead is whether the expected GDP growth rate should be regarded as if it is the same number across different countries. A well-known econometric method for dealing with this is referred to as “country fixed effects.” In this method, one uses the average for the Greek observations as an estimate of the Greek growth rate and the average of the U.S. observations as an estimate of the U.S. growth rate. This is a widely used procedure. By contrast, the weighting proposed by Herndon, Ash, and Pollin assumes that the expected growth rate is the same across different countries, an approach that is less widely chosen for panel data sets and in my opinion less to be recommended. Given that the ultimate goal in this case is to infer an average effect across different countries, I personally feel that a random-effects approach would be superior to fixed-effects estimation, particularly given the unbalanced nature of the panel (that is, given the fact that we have many more observations on the 90% debt state for some countries than for others). As I noted in my original piece, this would yield an estimate that would be in between those or RR and HAP. But to suggest that there is some deep flaw in the method used by RR or obvious advantage to the alternative favored by HAP is in my opinion quite unjustified.»
http://www.economonitor.com/blog/2013/04/reinhart-rogoff-and-herndon-ash-pollin-a-few-further-comments-2/
En todo caso la conclusión de RR no se basaba únicamente en la media de los 20 países avanzados desde 1946 a 2009. RR analizaba 3 sets de datos distintos con 2 métodos distintos en cada uno (media y mediana). HAP sólo critica uno de los 6 análisis en que se basa RR. De hecho, RR hace más hincapié en la mediana que en la media. A mí visualmente no me parece que ese 1% de diferencia en la mediana sea tan significativo como afirman y reafirman (en su respuesta a HAP) RR, y de hecho, la segunda parte que están preparando HAP pretende demostrar que el tramo superior al 90% es estadísticamente indistinguible de los dos anteriores:
“the purpose of the second half of our paper is to argue this point. In Table 4 we show that differences in average GDP growth in the categories 30-60 percent, 60-90 percent, and 90-120 percent cannot be statistically distinguished”
http://www.businessinsider.com/herndon-responds-to-reinhart-rogoff-2013-4#ixzz2S2X0SXbX
Y la tabla 4 es esta:
http://static4.businessinsider.com/image/5173d51e69bedd7e7c000045-527-474/herndon%20t%204.png