A estas alturas os habréis enterado, pero por si acaso os refrescaré la memoria: el CERN acaba de anunciar el descubrimiento del bosón de Higgs. No voy a escribir sobre el asunto porque ya lo han hecho muchos y muy bien. Sólo por poner algunos enlaces: Amazings.es, Francis, esmateria.com y este video subtitulado por mí.
En esencia, lo que han hecho en el CERN es encontrar el bosón de Higgs, una partícula que se había postulado para poder explicar por qué las partículas que existen en el Universo tienen la masa que tienen.
El problema es que el bosón de Higgs no tiene una firma clara, no sale claramente etiquetado en una foto. Se desintegra muy rápidamente, y lo único que podemos examinar es el resto que deja. Lo que hacen los aceleradores de partículas es lanzar un fantastillón de partículas contra otro fantastillón de partículas, hacerlas chocar y examinar los trozos que quedan. A partir de ahí se extrae información de tipo estadístico.
Y aquí está el problema. Para ponerle un ejemplo, imagine que tiene usted una moneda. Tiene sospechas de que está trucada, así que la lanza al aire unas cuantas veces a ver qué pasa. Con cinco lanzamientos, obtiene cinco caras. ¿Es eso prueba suficiente? Realmente no, ya que existe una probabilidad de un 3% de que el resultado se deba al azar. Si diez lanzamientos nos dan diez caras, ahora la probabilidad de que haya sucedido por azar es de una entre mil. Veinte lanzamientos, y decae a una entre un millón. Cuantas más veces hayamos hecho el lanzamiento de monedas, más sólidos serán los resultados.
Algo así pasa con el bosón de Higgs. Lo que se hizo fue observar y comparar con las predicciones de los actuales modelos teóricos. Hay diferencias entre uno y otro, pero ¿es lo bastante significativa? Para ilustrarlo, voy a robarle sin pudor algunas gráficas al bueno de Francis, cuyo blog sobre el tema es imprescindible (Fuente: aquí).

En el eje horizontal, tenemos la posible masa para el Higgs, y en el eje vertical una cantidad que nos indica la sección eficaz en unidades normalizadas. Para entendernos, si esa cantidad es mayor que uno, es indicativo de que allí «hay algo.» Por supuesto, ese algo puede ser otra partícula, así que tomamos el actual modelo de partículas (el llamado Modelo Estándar) y calculamos. El resultado es la línea de trazos (la que pone «Expected»). La línea continua («Observed») es el conjunto de observaciones. Como ven, en la zona de 125 GeV pasan dos cosas interesantes. La curva continua supera el valor 1, y además se separa de la predicción teórica. Si la curva experimental se separa de la teórica, es que aquí hay tomate. Pero ¿se separa lo suficiente? ¿Cuál es la probabilidad de que ese pico se corresponda con algo que NO sea el bosón de Higgs? ¿No es posible que estemos viendo una fluctuación estadística?
Para salir de dudas, usaremos la estadística. Es posible que la curva continua y la de trazos se hayan separado por azar, de modo similar a como las diez monedas pueden salirnos de cara por azar. Bien, pues hallemos la probabilidad de que nuestros datos difieran de la teoría por motivos de azar.
Lo que se hace es suponer que los datos se separan más o menos de su valor medio siguiendo lo que se llama una distribución gaussiana (o normal), de la que podéis aprender más donde siempre. Cada punto de la gráfica de arriba (por ejemplo, el de 125 GeV) es en realidad el conjunto de muchos datos, que se distribuyen siguiendo una gaussiana. Esta es la forma de una gaussiana (de Wikimedia Commons):
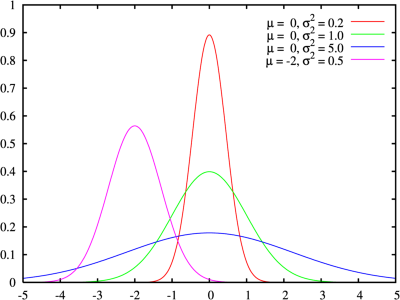
La forma matemática de esta función de probabilidad es: A*exp [ -(x-μ)2/2σ2]. Aquí x es la variable que estemos considerando, μ es el valor medio y σ es la anchura. Por cierto, σ es la letra griega sigma, así que atentos que por ahí van los tiros.
Fijaos en la curva roja, la que está centrada en x=0. Como puede verse a simple vista, los valores de x en el intervalo que va de -1 a +1 tiene casi todas las papeletas de estar en la distribución. O dicho de otro modo, la probabilidad de que yo mida un valor de x y me salga algo entre -1 y +1 es muy alta.
Ahora toca cuantificar cuánto es ese «muy alta.» La función de distribución normal tiene muchas propiedades matemáticas bien conocidas. Entre otras cosas, podemos calcular cómo de probable es que salga un número. Voy a saquear la Wikipedia de nuevo:

Fíjense en la parte azul oscuro, la que va desde -1σ a +1σ. La probabilidad de que un valor de x esté comprendido entre μ-σ y μ+σ es del 34,1+34,1 = 68,2% Es decir, aproximadamente dos de cada tres. Eso sería un resultado «a nivel un sigma.» ¿Y si admitimos como válidas las soluciones entre μ-2σ y μ+2σ? Entonces la probabilidad de que la solución sea válida sería del 95.4%
Volvamos a la primera gráfica:

Vean cómo la solución teórica («Expected») está envuelta en dos capas. La verde nos indica las soluciones con un nivel uno sigma; la amarilla, con un nivel dos sigma. Eso significa que, para el caso amarillo, la probabilidad de encontrar una señal que sea debida a una partícula y NO a un fenómeno aleatorio son del 95.4%. El pico de 125 GeV se escapa incluso de la zona de 2σ. Eso significa que ahí hay algo, y el bosón de Higgs tiene, digamos el 98% de las papeletas.
Eso parece bastante, pero no satisfactorio. Estamos hablando de una partícula que puede revolucionar nuestro conocimiento sobre el Universo. Decretar su existencia con un error de un 2% no es lo bastante tranquilizador. De hecho, cuando estos datos se hicieron públicos en 2011, la sensación de la comunidad científica fue algo así como «sí, no está nada mal, pero hay que afinar más.»
Dicho y hecho. El CERN se puso las pilas, observó más colisiones y filtró más datos. La meta es conseguir un pico lo bastante bueno. ¿Y qué es lo bastante bueno? Dándole vueltas a la manivela, podemos calcular la probabilidad de éxito en función del número de sigmas:
1 sigma: 68.26 %
2 sigmas: 95.44 %
3 sigmas: 99,73 %
4 sigmas: 99,995 %
5 sigmas: 99,99995 %
Podríamos seguir más y más, pero con esto basta. El consenso era que el nivel considerado como bueno sería el de cinco sigmas. De esa forma, la probabilidad de tener un pico debido a fluctuación estadística sería de una parte en un par de millones (Francis tiene un excelente artículo al respecto aquí). Aun así, los científicos de partículas trabajaban sobre hielo fino. Habían comprobado un gran rango de posibles masas, hasta más allá de 600 GeV, y la región de los 125 era de las pocas donde el bosón de Higgs podía esconderse. Si no se hallaba allí, mala cosa.
Pero la cosa iba bien. Los datos del instrumento CMS del CERN dieron en febrero de 2011 una señal a 125 GeV con un margen de 3,1σ, y ATLAS lo aumentó hasta 4,3σ. El Tevatron norteamericano registró una señal con 2,5 sigmas. Casi lo estaban logrando. Y esta mañana, el CERN anunció lo que todos estaban esperando: el descubrimiento de una nueva partícula a 5 sigmas. La masa de la nueva partícula se estima en unos 125,3 ± 0,6 GeV.
Una victoria de la estadística. Y de veinte años de trabajo, claro.
Nota adicional: en los procesos industriales se utiliza un método llamado «seis sigma» (six sigma). La idea es que los defectos en un proceso de fabricación caigan por debajo de una cierta cantidad. En eso, se supone que la curva de defectos (una gaussiana) se desplaza en una cantidad igual a 1,5σ. Las cifras de defectos para un «proceso seis sigma» difieren de las que aquí denominaríamos «seis sigmas,» pero en ambos casos tienen la curva de distribución gaussiana (o normal) como norma básica.



Chapeau, como siempre.
Gracias
Buena explicación 😉
Papá, a ver cuando publicas un post sobre el modelo atómico estándar, hablando de los tipos de partículas y eso…
Se agradece una explicación tan clara, entretenida y por demás interesante.
Saludos desde México
La verdad bastante esclarecedor e interesante.
Muchas gracias!
🙂
Bueno ya sabemos que lo han encontrado. En mil videos, blogs y demás (incluido el tuyo) vemos más o menos que es. La pregunta ahora es
¿Para que sirve? o ¿Para que servirá? ¿Que aplicaciones practicas, aunque sean por ahora ciencia ficción, le ves?
Imagina lo que puede suponer manipular un campo gravitatorio con la misma facilidad que manejamos un campo electromagnético. Puestos a imaginar, imagina mover un bloque de piedra de la pirámide de Giza (6 Tn), con la misma facilidad que te comunicas con un telefono móvil celular a 1000 km.
Saludos.
Javi
Fantástico Arturo, me ha encantado. En mi caso solo me falta saber para qué servirá exactamente el bosón de Higgs; cuáles serán sus aplicaciones en la vida real. Gracias de nuevo.
Pregunto lo mismo que «anónimo», más allá de lo maravilloso e incluso espiritual que puede ser este descubrimiento, no sé en qué lo quieren aplicar… si son simplemente curiosos que en vez de rezar se pusieron a hacer chocar partículas, o si tienen algún objetivo ético en el asunto, salute
Gracias, muy bueno! Saludos desde Costa Rica
Por favor profesor explique la utilidad, no del boson de Higgs, sino del antiboson…
Excelente explicación. Física, y estadísticas, entendibles.
Sin ánimo de ofender, «flipo» con las personas que preguntan sobre la utilidad. Lo mismo podrían haberle preguntado a Newton sobre sus leyes, ¿qué utilidad tenían entonces?. Ninguna.
¿Y ahora?. No podríamos construir estructuras complejas, edificios, puentes. No podríamos construir aviones. Cálculos sobre canalizaciones de agua, etc., serían imposibles. No tendríamos satélites (GPS, fotografía, rescate, transmisiones, estudio del clima, etc.). No podríamos ni siquiera construir grandes barcos (cómo petroleros) de forma eficiente.
¿Qué utilidad tenían las leyes de Maxwell?. Tampoco ninguna…..
Ay!…..
Muy buena explicación. Pero tengo algunas preguntas que quizá sean algo ingenuas, cuando se dice que «La masa de la nueva partícula se estima en unos 125,3 ± 0,6 GeV.» De que tipo de masa se está hablando?, no es esta partícula la responsable de la masa de las otras ya mas conocidas? Y si es que dura tan poco, como es que permite la interacción entre las demás partículas de un modo mas o menos continuo y fuera de un laboratorio? Saludos.
¡Qué buena explicación!
en este sitio un uso de la física cuántica para la vida real: http://www.diegoelduende.blogspot.com
Sigma no es esto, me dejaste…
1 sigma= 690.000 DPMO = 32% de eficiencia
2 sigma= 308.538 DPMO = 69% de eficiencia
3 sigma= 66.807 DPMO = 93,3% de eficiencia
4 sigma= 6.210 DPMO = 99,38% de eficiencia
5 sigma= 233 DPMO = 99,977% de eficiencia
6 sigma= 3,4 DPMO = 99,99966% de eficiencia
7 sigma= 0,019 DPMO = 99,9999981% de eficiencial
Un apunte, el motivo por el que se estableció en 5 sigma es por el tamaño de la muestra, en otros campos de la ciencia (incluida la física que no sea de partículas) con 2 sigma es suficiente, porque las muestras son más pequeñas.
Un momento, ¿no se suponía que cuanta más muestra mejor? Sí porque reduce el error de tipo II (decir que no hay diferencias cuando sí las hay), pero a la vez aumenta el error de tipo I. Con una muestra de millones y millones como son habituales en el CERN, el error tipo I es alto, por lo tanto hay que elevar el nivel de significancia, ya que es fácil encontrar diferencias donde no las hay.
Pero no porque sea algo que vaya a revolucionar nuestro conocimiento del universo, sino única y exclusivamente por el tamaño de la muestra.